题目内容

10．如图所示，请将图中的“蘑菇”向左平移6个格，再向下平移2个格．

分析 利用平移的性质分别得出对应点位置，进而得出答案．

解答 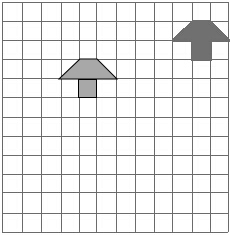解：如图所示：

点评 此题主要考查了利用平移设计图案，根据题意得出对应点平移后位置是解题关键．

练习册系列答案
相关题目
20．（1）计算   （-$\frac{1}{2}$）-2+$\root{3}{8}$-|1-tan60°|+π0
（2）解不等式组$\left\{\begin{array}{l}{x+1＞0}\\{1-\frac{1}{3}×＞0}\end{array}\right.$  并把解集在数轴上表示出来．
1．（1）计算：$|{-3}|+\sqrt{3}•tan30$°-$\root{3}{8}$-（2013-π）0+${（{\frac{1}{3}}）^{-1}}$
（2）解方程：x（x+4）=-3（4+x）．
18．观察下表
列　　　举猜　　　想
3、4、532=4+5
5、12、1352=12+13
7、24、2572=24+25
……
13、b、c132=b+c
请你结合该表格及相关知识，求出b，c的值，并验证13，b，c是否是勾股数？
5．已知P1（x1，y1），P2（x2，y2），P（x3，y3）是反比例函数$y=\frac{k^2}{x}$（k≠0）的图象上的三点，且x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（　　）
A．y3＜y2＜y1B．y2＜y1＜y3C．y1＜y2＜y3D．y2＜y3＜y1
15．在建筑楼梯时，设计者要考虑楼梯的安全程度，如图1，虚线为楼梯的斜度线，斜度线与地板的夹角为倾角θ，一般情况下，倾角θ 愈小，楼梯的安全程度愈高．如图2，设计者为提高楼梯的安全程度，要把楼梯的倾角由θ1减至θ2，这样楼梯占用地板的长度由d1增加到d2，已知d1=4m，∠θ1=45°，∠θ2=36°
求楼梯占用地板的长度增加了多少？（精确到0.01m）
参考数据：
sin36°=0.5878
tan36°=0.7265
cos36°=0.8090．
2．已知直角坐标系中，点A（5，1），B（0，4），则AB=$\sqrt{34}$．
19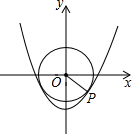．如图，已知二次函数的解析式为y=x2-1，其图象上有一个动点P，连接OP（O为坐标原点），并以OP为半径作圆，则该圆的最小面积是（　　）
A．$\frac{1}{2}$πB．$\frac{3}{4}$πC．πD．$\frac{9}{16}$π
20．下列运算中，正确的是（　　）
A．5m-m=4B．（m2）4=m8C．-（m-n）=m+nD．m2÷m2=m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网