题目内容
等边△ABC边长为5,D是边BC上一点,且BD=2,M、N分别是AB、AC上的两个动点,当M点在AB上运动时,保持∠MDN=60°,设BM=x,CN=y,(1)求y与x之间的函数关系式并求出自变量x的取值范围.
(2)连接MN,当M点运动到什么位置时,△MDN是等边三角形;
(3)连接MN,当△MDN是直角三角形时,求此时x的值.

【答案】分析:(1)根据等边三角形的性质和已知条件可证△BMD∽△CDN,根据相似三角形的性质即可得出y与x之间的函数关系式;
(2)根据相似三角形的性质和等边三角形的判定即可得到M点运动的位置;
(3)分①当∠DMN=90°时,∠MND=30°;②当∠DNM=90°时,∠DMN=30°两种情况讨论即可得到当△MDN是直角三角形时x的值.
解答:解:(1)∵△ABC是等边三角形,
∴AB=BC=AC=5,∠B=∠C=60°,
∵∠BMD=180°-∠B-∠BDM,∠CDN=180°-∠MDN-∠BDM
∴∠BMD=∠CDN,
∴△BMD∽△CDN,
∴ ,
,
∵BD=2,
∴CD=5-2=3,
∴ ,
,
∴ ,
,
由题意知,x≤5,y≤5;当y≤5时,
∴自变量x的取值范围是:1.2≤x≤5;
(2)当BM=3时,△MDN是等边三角形,理由如下:
∵△BMD∽△CDN,
∴ ,
,
∵BM=CD=3,
∴MD=DN,
∵∠MDN=60°,
∴△MDN是等边三角形;
(3)∵△BMD∽△CDN,
∴ ,
,
①当∠DMN=90°时,∠MND=30°,
∴ ,
,
∴ ,
,
∴ ;
;
②当∠DNM=90°时,∠DMN=30°,
∴DM=2DN
∴ ,
,
∴x=6,
由(1)知1.2≤x≤5知不合题意舍去.
综合①②可知,当△MDN是直角三角形时,x的值为 .
.
点评:本题考查的是相似形综合题,此题涉及到等边三角形的判定和性质、相似三角形的判定与性质,函数思想和分类思想,有一定的综合性,难度适中.
(2)根据相似三角形的性质和等边三角形的判定即可得到M点运动的位置;
(3)分①当∠DMN=90°时,∠MND=30°;②当∠DNM=90°时,∠DMN=30°两种情况讨论即可得到当△MDN是直角三角形时x的值.
解答:解:(1)∵△ABC是等边三角形,
∴AB=BC=AC=5,∠B=∠C=60°,
∵∠BMD=180°-∠B-∠BDM,∠CDN=180°-∠MDN-∠BDM
∴∠BMD=∠CDN,
∴△BMD∽△CDN,
∴
 ,
,∵BD=2,
∴CD=5-2=3,
∴
 ,
,∴
 ,
,由题意知,x≤5,y≤5;当y≤5时,

∴自变量x的取值范围是:1.2≤x≤5;
(2)当BM=3时,△MDN是等边三角形,理由如下:
∵△BMD∽△CDN,
∴
 ,
,∵BM=CD=3,
∴MD=DN,
∵∠MDN=60°,
∴△MDN是等边三角形;
(3)∵△BMD∽△CDN,
∴
 ,
,①当∠DMN=90°时,∠MND=30°,
∴
 ,
,∴
 ,
,∴
 ;
;②当∠DNM=90°时,∠DMN=30°,
∴DM=2DN
∴
 ,
,∴x=6,
由(1)知1.2≤x≤5知不合题意舍去.
综合①②可知,当△MDN是直角三角形时,x的值为
 .
.点评:本题考查的是相似形综合题,此题涉及到等边三角形的判定和性质、相似三角形的判定与性质,函数思想和分类思想,有一定的综合性,难度适中.

练习册系列答案
相关题目
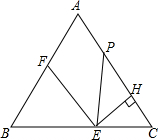 如图,等边△ABC边长为4,E是边BC上动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).
如图,等边△ABC边长为4,E是边BC上动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2). 7、如图,等边△ABC边长为3cm,将△ABC沿AC向右平移1cm,得到△DEF,则四边形ABEF的周长( )
7、如图,等边△ABC边长为3cm,将△ABC沿AC向右平移1cm,得到△DEF,则四边形ABEF的周长( ) 14、如图,已知等边△ABC边长为1,D是△ABC外一点且∠BDC=120°,BD=CD,∠MDN=60°.
14、如图,已知等边△ABC边长为1,D是△ABC外一点且∠BDC=120°,BD=CD,∠MDN=60°. 如图,等边△ABC边长为10cm,以AB为直径的⊙O分别交CA、CB于D、E两点,则图中阴影部分的面积(结果保留π)是
如图,等边△ABC边长为10cm,以AB为直径的⊙O分别交CA、CB于D、E两点,则图中阴影部分的面积(结果保留π)是