题目内容
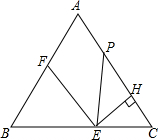 如图,等边△ABC边长为4,E是边BC上动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).
如图,等边△ABC边长为4,E是边BC上动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线);
(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ的面积(用含x的代数式表示);
(3)当(2)中的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围.
分析:(1)根据三角形ABC是等边三角形和EF∥AC,可得等边三角形BEF,则可写出与EF相等的线段;
(2)根据(1)可知EF=BE=4-x,要求平行四边形的面积,只需求得EF边上的高.作EH⊥AC于H,根据30度的直角三角形EHC进行表示EH的长,进一步求得平行四边形的面积;
(3)根据二次函数的顶点式或顶点的公式法求得平行四边形的面积的最大值时x的值,分析平行四边形的位置和形状.然后根据公共点的个数分析圆和平行四边形的各边的位置关系,进一步根据圆和直线的位置关系求得r的取值范围.
(2)根据(1)可知EF=BE=4-x,要求平行四边形的面积,只需求得EF边上的高.作EH⊥AC于H,根据30度的直角三角形EHC进行表示EH的长,进一步求得平行四边形的面积;
(3)根据二次函数的顶点式或顶点的公式法求得平行四边形的面积的最大值时x的值,分析平行四边形的位置和形状.然后根据公共点的个数分析圆和平行四边形的各边的位置关系,进一步根据圆和直线的位置关系求得r的取值范围.
解答: 解:(1)BE、PE、BF三条线段中任选两条.
解:(1)BE、PE、BF三条线段中任选两条.
(2)连接FP,作EQ∥FP交FE于E
设EC为x
∵EH⊥AC,
∴∠EHC=90°
∴△CHE为直角三角形
∵△ABC为等边三角形,
∴∠C=60°
在Rt△CHE中,∠CHE=90°,∠C=60°,
∠HEC=180°-∠C-∠EHC=30°
∴2HC=EC
∵HE2=EC2-HC2
∴EH=
x,
∵EF∥AC,FP∥EQ
∴四边形EFPQ为平行四边形
∴PQ=FE
又∵PE=BE
∴PQ=EF=BE=4-x
∴S平行四边形EFPQ=-
x2+2
x.
(3)S平行四边形EFPQ=-
x2+2
x
=-
(x-2)2+2
,
∴当x=2时,S平行四边形EFPQ有最大值.
此时E、F、P分别为△ABC三边BC、AB、AC的中点,且点C、点Q重合
∴平行四边形EFPQ是菱形.
过E点作ED⊥FP于D,
∴ED=EH=
.
∴当⊙E与平行四边形EFPQ四条边交点的总个数是2个时,0<r<
;
当⊙E与平行四边形EFPQ四条边交点的总个数是4个时,r=
;
当⊙E与平行四边形EFPQ四条边交点的总个数是6个时,
<r<2;
当⊙E与平行四边形EFPQ四条边交点的总个数是3个时,r=2;
当⊙E与平行四边形EFPQ四条边交点的总个数是0个时,r>2.
 解:(1)BE、PE、BF三条线段中任选两条.
解:(1)BE、PE、BF三条线段中任选两条.(2)连接FP,作EQ∥FP交FE于E
设EC为x
∵EH⊥AC,
∴∠EHC=90°
∴△CHE为直角三角形
∵△ABC为等边三角形,
∴∠C=60°
在Rt△CHE中,∠CHE=90°,∠C=60°,
∠HEC=180°-∠C-∠EHC=30°
∴2HC=EC
∵HE2=EC2-HC2
∴EH=
| ||
| 2 |
∵EF∥AC,FP∥EQ
∴四边形EFPQ为平行四边形
∴PQ=FE
又∵PE=BE
∴PQ=EF=BE=4-x
∴S平行四边形EFPQ=-
| ||
| 2 |
| 3 |
(3)S平行四边形EFPQ=-
| ||
| 2 |
| 3 |
=-
| ||
| 2 |
| 3 |

∴当x=2时,S平行四边形EFPQ有最大值.
此时E、F、P分别为△ABC三边BC、AB、AC的中点,且点C、点Q重合
∴平行四边形EFPQ是菱形.
过E点作ED⊥FP于D,
∴ED=EH=
| 3 |
∴当⊙E与平行四边形EFPQ四条边交点的总个数是2个时,0<r<
| 3 |
当⊙E与平行四边形EFPQ四条边交点的总个数是4个时,r=
| 3 |
当⊙E与平行四边形EFPQ四条边交点的总个数是6个时,
| 3 |
当⊙E与平行四边形EFPQ四条边交点的总个数是3个时,r=2;
当⊙E与平行四边形EFPQ四条边交点的总个数是0个时,r>2.
点评:综合运用了等边三角形的判定和性质、解直角三角形的知识、直线和圆的位置关系与数量关系之间的联系.

练习册系列答案
相关题目
 如图,等边△ABC,G是△ABC的重心,直线AG把△ABC分成面积相等的两部分,但是不是过G点的任意一条直线都把△ABC分成面积相等的两部分?用实验或说理的方法,给予探索并得出结论.
如图,等边△ABC,G是△ABC的重心,直线AG把△ABC分成面积相等的两部分,但是不是过G点的任意一条直线都把△ABC分成面积相等的两部分?用实验或说理的方法,给予探索并得出结论. 7、如图,等边△ABC边长为3cm,将△ABC沿AC向右平移1cm,得到△DEF,则四边形ABEF的周长( )
7、如图,等边△ABC边长为3cm,将△ABC沿AC向右平移1cm,得到△DEF,则四边形ABEF的周长( ) 如图,等边△ABC边长为10cm,以AB为直径的⊙O分别交CA、CB于D、E两点,则图中阴影部分的面积(结果保留π)是
如图,等边△ABC边长为10cm,以AB为直径的⊙O分别交CA、CB于D、E两点,则图中阴影部分的面积(结果保留π)是 (2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
(2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )