题目内容
 如图,在直角坐标系中,A(-3,4),B(-1,-2),O为坐标原点,把△AOB向右平移3个单位,得到△DEF.
如图,在直角坐标系中,A(-3,4),B(-1,-2),O为坐标原点,把△AOB向右平移3个单位,得到△DEF.(1)求D、E、F三点的坐标.
(2)求△DEF的面积.
考点:坐标与图形变化-平移
专题:
分析:(1)利用平移规律得出各点坐标即可;
(2)利用S梯形ABED-S△ADO-S△BEO进而求出即可.
(2)利用S梯形ABED-S△ADO-S△BEO进而求出即可.
解答: 解:(1)∵A(-3,4),B(-1,-2),O为坐标原点,把△AOB向右平移3个单位,得到△DEF;
解:(1)∵A(-3,4),B(-1,-2),O为坐标原点,把△AOB向右平移3个单位,得到△DEF;
∴D(0,4),E(2,-2),F(3,0);
(2)过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,
∵△AOB的面积等于△DEF的面积,
∴△DEF的面积=
(3+1)×6-
×3×4-
×1×2=5.
 解:(1)∵A(-3,4),B(-1,-2),O为坐标原点,把△AOB向右平移3个单位,得到△DEF;
解:(1)∵A(-3,4),B(-1,-2),O为坐标原点,把△AOB向右平移3个单位,得到△DEF;∴D(0,4),E(2,-2),F(3,0);
(2)过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,
∵△AOB的面积等于△DEF的面积,
∴△DEF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了坐标与图形变化以及三角形面积求法,利用特殊面积转化求出△DEF的面积是解题关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
在直角坐标系中,O为坐标原点A(1,3),在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P共有( )
| A、4个 | B、3个 | C、2个 | D、5个 |
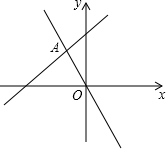 如图,函数y=-2x和y=kx+b的图象相交于点A(m,3),则关于x的不等式kx+b+2x>0的解集为( )
如图,函数y=-2x和y=kx+b的图象相交于点A(m,3),则关于x的不等式kx+b+2x>0的解集为( )A、x>
| ||
| B、x<m | ||
| C、x>m | ||
D、x>-
|