题目内容
3.若顺次连接平行四边形ABCD各边中点所得四边形必定是( )| A. | 矩形 | B. | 平行四边形 | C. | 正方形 | D. | 菱形 |
分析 连接平行四边形的一条对角线,根据中位线定理,可得新四边形的一组对边平行且等于对角线的一半,即一组对边平行且相等.则新四边形是平行四边形.
解答  解:顺次连接平行四边形ABCD各边中点所得四边形必定是:平行四边形,
解:顺次连接平行四边形ABCD各边中点所得四边形必定是:平行四边形,
理由如下:
(如图)根据中位线定理可得:GF=$\frac{1}{2}$BD且GF∥BD,EH=$\frac{1}{2}$BD且EH∥BD,
∴EH=FG,EH∥FG,
∴四边形EFGH是平行四边形.
故选B.
点评 本题考查了平行四边形的判定和三角形的中位线定理得应用,通过做此题培养了学生的推理能力,题目比较好,难度适中.

练习册系列答案
相关题目
14.已知一组数据:18,12,5,10,5,16,这组数据的中位数和众数分别是( )
| A. | 11,5 | B. | 7.5,5 | C. | 7.5,18 | D. | 11,18 |
13.体育课上,老师测量小明跳远成绩的依据是( )
| A. | 过直线上一点且垂直于这条直线的直线有且只有一条 | |
| B. | 两点之间,线段最短 | |
| C. | 垂线段最短 | |
| D. | 两点确定一条直线 |
 一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数(含备用零钱)y的关系,如图所示,结合图象回答下列问题:
一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数(含备用零钱)y的关系,如图所示,结合图象回答下列问题: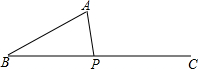 如图,已知∠A=30°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP=$\sqrt{3}$或$\frac{4}{3}$$\sqrt{3}$cm时,△BAP为直角三角形.
如图,已知∠A=30°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP=$\sqrt{3}$或$\frac{4}{3}$$\sqrt{3}$cm时,△BAP为直角三角形.