题目内容
在四边形
中，对角线AC与BD交于点O，△ABO≌△CDO.
（1）求证：四边形为平行四边形；
（2）若∠ABO=∠DCO，求证：四边形为矩形.
解：（1）证明：∵△ABO≌△CDO
∴AO=CO，BO=DO
∴AC、BD互相平分
∴四边形ABCD是平行四边形
（2）证明：∵四边形ABCD是平行四边形
∴AB∥CD，∴∠ABO=∠CDO
∵∠ABO=∠DCO，
∴∠DCO =∠CDO
∴CO=DO
∵△ABO≌△CDO
∴AO=CO，BO=DO ∴AO=CO=BO=DO
即AC=BD
∴□ABCD是矩形
解析
练习册系列答案
相关题目
中，对角线AC与BD交于点O，△ABO≌△CDO.
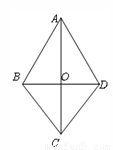
中，对角线AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有【
】
中，对角线
平分
．
，
时，求证：
；
与
互补时，线段
有怎样的数量关系?写出你的猜想，并给予证明；
，
中，对角线AC与BD交于点O，△ABO≌△CDO.
中，对角线
与
互相平分，交点为
．在不添加任何辅助线的前提下，要使四边形