题目内容
6.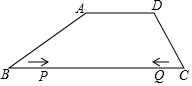 如图,四边形ABCD中,AD∥BC,AD=5cm,AB=$\sqrt{46}$cm,BC=13cm,DC=$\sqrt{30}$cm.在BC上有动点P、Q,P从B到C,以2cm/s的速度运动,Q从C到B,以1cm/s的速度同时开始运动,当P到达终点时,Q也立刻停止,设运动的时间为t(s).
如图,四边形ABCD中,AD∥BC,AD=5cm,AB=$\sqrt{46}$cm,BC=13cm,DC=$\sqrt{30}$cm.在BC上有动点P、Q,P从B到C,以2cm/s的速度运动,Q从C到B,以1cm/s的速度同时开始运动,当P到达终点时,Q也立刻停止,设运动的时间为t(s).(1)t的取值范围是0≤t≤$\frac{13}{2}$;
(2)如果PQ的长为y(cm),求y关于t的函数解析式;
(3)求当t为多少时,以A、D、P、Q为顶点的凸四边形是平行四边形;
(4)以A、D、P、Q为顶点的凸四边形是否为菱形?如果是,求出相应的t,如果不是,说出理由.
分析 (1)由距离除以速度求出最大的时间,即可得出结论;
(2)先求出点P,Q相遇的时间,再分相遇前和相遇后两种情况即可得出结论;
(3)分两种情况,利用平行四边形的性质即可得出结论;
(4)先求出AE和BE,再分两种情况计算判断即可得出结论.
解答 解:(1)∵BC=13,点P的速度时2cm/s,
∴t最大=13÷2=$\frac{13}{2}$,
∴0≤t≤$\frac{13}{2}$,
故答案为0≤t≤$\frac{13}{2}$;
(2)当点P和Q相遇时,BP+CQ=13,
由运动知,BP=2t,CQ=t,
∴2t+t=13,
∴t=$\frac{13}{3}$,
当0≤t≤$\frac{13}{3}$时,BP+PQ+CQ=13,
∴2t+y+t=13,
∴y=-3t+13,
当$\frac{13}{3}$<t≤$\frac{13}{2}$时,PQ=BP+CQ-BC,
∴y=2t+t-13=3t-13;
(3)当0≤t≤$\frac{13}{3}$时,如图1,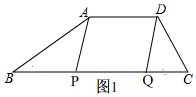
∵四边形ADQP是平行四边形,
∴PQ=AD,
∴-3t+13=5,
∴t=$\frac{8}{3}$,
当$\frac{13}{3}$<t≤$\frac{13}{2}$时,如图2,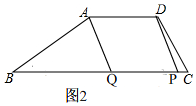 ∵四边形ADPQ是平行四边形,
∵四边形ADPQ是平行四边形,
∴PQ=AD,
∴3t-13=5,
∴t=6;
即:t=$\frac{8}{3}$或6时,以A、D、P、Q为顶点的凸四边形是平行四边形;
(4)如图3,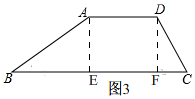
过点A作AE⊥BC,过点D作DF⊥BC于F,
∴四边形AEFD是矩形,
∴EF=AD=5,AE=DF,
∴BE+CF=8,
在Rt△ABE中,AE2=AB2-BE2,
在Rt△CDF中,AE2=CD2-DF2,
∴46-BE2=30-(8-BE)2,
∴BE=5,
∴CF=3,
∴AE=DF=$\sqrt{21}$
当0≤t≤$\frac{13}{3}$时,如图5,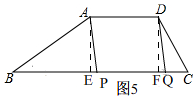 假设以A、D、P、Q为顶点的凸四边形能为菱形,
假设以A、D、P、Q为顶点的凸四边形能为菱形,
∴t=$\frac{8}{3}$,且AP=AD=5,
∴BP=2t=$\frac{16}{3}$,
∴PE=BP-BE=$\frac{1}{3}$,
在Rt△APE中,AP=$\sqrt{A{E}^{2}-P{E}^{2}}$=$\sqrt{21-\frac{1}{9}}$≠5,
此种情况四边形ADQP不能是菱形;
当$\frac{13}{3}$<t≤$\frac{13}{2}$时,如图4,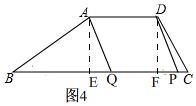
假设以A、D、P、Q为顶点的凸四边形能为菱形,
∴t=6,且AP=AQ=5,
∴BQ=BC-CQ=13-6=7,
∴EQ=BQ-BE=2,
在Rt△AQE中,AQ=$\sqrt{A{E}^{2}+E{Q}^{2}}$=$\sqrt{21+4}$=5,
∴四边形ADPQ是菱形;
即:t=6时,以A、D、P、Q为顶点的凸四边形是菱形.
点评 此题是四边形综合题,主要考查了梯形的性质,平行四边形的性质,菱形的性质,解(2)的关键是求出点P,Q相遇时的时间,解(3)的关键是分类讨论的思想解决问题,解(4)的关键是构造直角三角形.

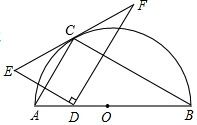 如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为5$\sqrt{3}$;③当AD=3时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=5;⑤当点D从点A运动到B点时,线段EF扫过的面积是20$\sqrt{3}$.其中正确结论的序号是①②④.
如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为5$\sqrt{3}$;③当AD=3时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=5;⑤当点D从点A运动到B点时,线段EF扫过的面积是20$\sqrt{3}$.其中正确结论的序号是①②④.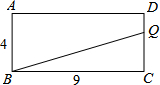 如图,长方形ABCD中,AB=4,BC=9,动点Q沿着C→D→A→B的方向运动至点B停止,设点Q运动的路程为x,△QCB的面积为y.
如图,长方形ABCD中,AB=4,BC=9,动点Q沿着C→D→A→B的方向运动至点B停止,设点Q运动的路程为x,△QCB的面积为y.
 已知,如图,在四边形ABCD中,AC、BD交于点O,AD∥BC,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AB=CD;并给出证明.
已知,如图,在四边形ABCD中,AC、BD交于点O,AD∥BC,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AB=CD;并给出证明.