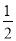题目内容
5.当m,n是正实数,且满足m+n=mn时,就称点P(m,$\frac{m}{n}$)为“友谊点”.已知点A(0,5)与点M都在直线y=-x+b上,点B,C是“友谊点”,且点B在线段AM上.(1)点B的坐标为(3,2);
(2)若MC=$\sqrt{3}$,AM=4$\sqrt{2}$,则△MBC的面积为$\frac{\sqrt{2}}{2}$.
分析 (1)由m+n=mn变式为$\frac{m}{n}$=m-1,可知P(m,m-1),所以在直线y=x-1上,点A(0,5)在直线y=-x+b上,求得直线AM:y=-x+5,进而求得B(3,2);
(2)根据直线平行的性质从而证得直线AM与直线y=x-1垂直,然后根据勾股定理求得BC的长,从而求得三角形的面积.
解答 解:(1)∵m+n=mn且m,n是正实数,
∴$\frac{m}{n}$+1=m,即$\frac{m}{n}$=m-1,
∴P(m,m-1),
即“友谊点”B在直线y=x-1上,
∵点A(0,5)在直线y=-x+b上,
∴b=5,
∴y=-x+5,
∵“友谊点”B在直线y=-x+5上,
∴由$\left\{\begin{array}{l}{y=x-1}\\{y=-x+5}\end{array}\right.$解得$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$,
∴B(3,2);
故答案为(3,2).
(2)∵一、三象限的角平分线y=x垂直于二、四象限的角平分线y=-x,而直线y=x-1与直线y=x平行,直线y=-x+5与直线y=-x平行,
∴直线AM与直线y=x-1垂直,
∵点B是直线y=x-1与直线AM的交点,
∴垂足是点B,
∵点C是“友谊点”,
∴点C在直线y=x-1上,
∴△MBC是直角三角形,
∵B(3,2),A(0,5),
∴AB=3$\sqrt{2}$,
∵AM=4$\sqrt{2}$,
∴BM=$\sqrt{2}$,
又∵CM=$\sqrt{3}$,
∴BC=1,
∴S△MBC=$\frac{1}{2}$BM•BC=$\frac{\sqrt{2}}{2}$.
故答案为$\frac{\sqrt{2}}{2}$.
点评 本题考查了一次函数的性质,直角三角形的判定,勾股定理的应用以及三角形面积的计算等,判断直线垂直,借助正比例函数是本题的关键.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. | (a-b)2=-(b-a)2 | B. | $\frac{1}{{x}^{3}}$=x-3 | C. | $\frac{{a}^{2}+1}{a+1}$=a+1 | D. | x6÷x2=x3 |
| A. | (-3a)2=-9a2 | B. | $\frac{-a+b}{a+b}$=-1 | C. | 2a2-1=(2a+1)(2a-1) | D. | a3-4a3=-3a3 |
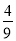 B.
B. 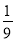 C.
C. 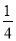 D.
D.