题目内容
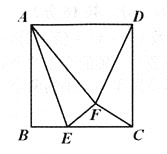
【题目】如图,点E是边长为2的正方形ABCD的边BC上的一动点(不与端点重合),将△ABE沿AE翻折至△AFE的位置,若△CDF是等腰三角形,则BE=________.
【答案】![]() 或
或![]()
【解析】
以CF=DF和CD=DF两种情形分别画出图形,然后再求解即可。
解:如图

①当CF=DF时,则F在CD垂直平分线上,
如图1,作CD的垂直平分线交AB、DC于M、N,作FGLCD于G,则AM=BM=FG=1,+
由翻折可知,BE=EF,AF=AB=2,
∴在△AMF中,由勾股定理BG=FM=![]() ,
,
∴![]() ,
,![]() ,
,![]() ;.
;.
②当CD=DF时,则△ADF是等边三角形,F在BC垂直平分线上,
如图2:作BC的垂直平分线交AD、BC于M、N,
∵FM=![]() ,FN=2-
,FN=2-![]() ,
,![]() ,
,
∴![]() ,
,
∴BE=3-![]()
故答案为![]() 或
或![]() .
.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
【题目】如图,一艘海轮位于灯塔P的北偏东55方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
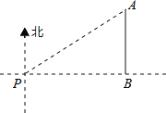
A.2cos55o海里B.![]() 海里C.2sin55海里D.
海里C.2sin55海里D.![]() 海里
海里
【题目】小明同学利用寒假30天时间贩卖草莓,了解到某品种草莓成本为10元/千克,在第![]() 天的销售量与销售单价如下(每天内单价和销售量保持一致):
天的销售量与销售单价如下(每天内单价和销售量保持一致):
销售量 |
|
销售单价 | 当 |
当 |
设第![]() 天的利润
天的利润![]() 元.
元.
(1)请计算第几天该品种草莓的销售单价为25元/千克?
(2)这30天中,该同学第几天获得的利润最大?最大利润是多少?注:利润=(售价-成本)×销售量