Question

【题目】 问题与探索

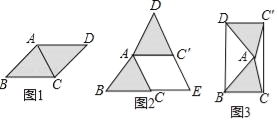
问题情境：课堂上，老师让同学们以“菱形纸片的剪拼”为主题开展数学活动．如图（1），将一张菱形纸片ABCD（∠BAD＞90°）沿对角线AC剪开，得到△ABC和△ACD．

操作发现：

（1）将图（1）中的△ACD以点A为旋转中心，按逆时针方向旋转角α，使α=∠BAC，得到如图（2）所示的△AC′D，分别延长BC和DC′交于点E，则四边形ACEC′的形状是 ．

（2）创新小组将图（1）中的△ACD以点A为旋转中心，按逆时针方向旋转角α，使α=2∠BAC，得到如图（3）所示的△AC′D，连接DB、C′C，得到四边形BCC′D，发现它是矩形，请证明这个结论．

Answer 1

【答案】(1)菱形；(2)证明过程见解析

【解析】

试题分析：(1)、结论：菱形．首先证明四边形ACEC′是平行四边形，再由AC=AC′即可证明结论．

(2)、如图3中，过点A作AE⊥C′C于点E，首先证明DC′∥CB，DC′=BC，推出四边形BCC′D是平行四边形，再证明∠BCC′=900即可．

试题解析：(1)、结论：菱形．理由：如图2中，

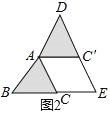
由题意∵AB=BC， ∴∠BAC=∠BCA=∠CAC′=∠AC′D ∴AC′∥EC， ∵∠CAC′=∠AC′D，

∴AC∥EC′， ∴四边形ACEC′是平行四边形， ∵AC=AC′， ∴四边形ACEC′是菱形．

(2)、如图3中，过点A作AE⊥C′C于点E，

由旋转的性质，得AC′=AC， ∴∠CAE=∠C′AE=α=∠ABC，∠AEC=90°， ∵BA=BC，

∴∠BCA=∠BAC ∴∠CAE=∠BCA， ∴AE∥BC． 同理，AE∥DC′， ∴BC∥DC′，

又∵BC=DC′， ∴四边形BCC′D是平行四边形， 又∵AE∥BC，∠AEC=90°，

∴∠BCC′=1800﹣900=900 ∴四边形BCC′D是矩形．