题目内容
某产品每件成本80元,试销阶段每件产品的销售价(元)与品的日销售量(件)之间的关系如下表:
如果日销售量y与销售价x的关系为y=kx+b.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少?
| x(元) | … | 150 | 200 | … |
| y(件) | … | 25 | 20 | … |
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少?
考点:二次函数的应用
专题:
分析:(1)本题属于市场营销问题,销售利润=一件利润×销售件数,一件利润=销售价-成本,日销售量y是销售价x的一次函数,所获利润W为二次函数.
(2)运用二次函数的性质,可求最大利润.
(2)运用二次函数的性质,可求最大利润.
解答:解:(1)设此一次函数关系式为y=kx+b,
则
,
解得:
.
故一次函数的关系式为y=-
x+40.
(2)设所获利润为W元,
则W=(x-80)(-
x+40)
=-
x2+120x-3200
=-
(x-240)2+2540,
所以产品的销售价应定为240元时,此时每日的销售利润最大为2540元.
则
|
解得:
|
故一次函数的关系式为y=-
| 1 |
| 10 |
(2)设所获利润为W元,
则W=(x-80)(-
| 1 |
| 10 |
=-
| 1 |
| 10 |
=-
| 1 |
| 10 |
所以产品的销售价应定为240元时,此时每日的销售利润最大为2540元.
点评:此题主要考查了一次函数,二次函数的求法以及二次函数性质的运用,需要根据题意,逐步求解,由易到难,搞清楚这两个函数之间的联系.

练习册系列答案
相关题目
为了了解某市5万名初中毕业生的中考数学成绩,从中抽取1000名学生的数学成绩进行统计分析,在这个问题中下列说法正确的是( )
| A、总体是某市5万名初中毕业生 |
| B、个体是每个初中毕业生的数学成绩 |
| C、样本是从中抽取1000名学生 |
| D、样本容量是1000名 |
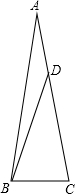 如图,△ABC中,∠A=20°,AB=AC,D是AC上一点,AD=BC,求∠DBA的度数.
如图,△ABC中,∠A=20°,AB=AC,D是AC上一点,AD=BC,求∠DBA的度数. 一个拱形桥洞成抛物线形,它的截面如图.现测得,桥洞顶点O与水面DE的距离为1m,桥洞的水面宽ED=3m,当水位下降到桥洞顶点O与水面AB的距离为3m时,这时水面宽AB是多少m?
一个拱形桥洞成抛物线形,它的截面如图.现测得,桥洞顶点O与水面DE的距离为1m,桥洞的水面宽ED=3m,当水位下降到桥洞顶点O与水面AB的距离为3m时,这时水面宽AB是多少m? 将方格中的帽子图形分别作以下变换:
将方格中的帽子图形分别作以下变换: 如图:地面上棱长为10的正方体两个相距最远的顶点A处有一只苍蝇、顶点B处有一只蜘蛛,为尽快将苍蝇吃掉,这只蜘蛛想沿着正方体的表面走一条最近的路线爬到苍蝇的落脚点,则蜘蛛所走的最短路线长度是多少?
如图:地面上棱长为10的正方体两个相距最远的顶点A处有一只苍蝇、顶点B处有一只蜘蛛,为尽快将苍蝇吃掉,这只蜘蛛想沿着正方体的表面走一条最近的路线爬到苍蝇的落脚点,则蜘蛛所走的最短路线长度是多少?