题目内容
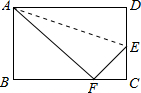已知，如图，折叠长方形的一边AD使点D落在BC边的点F处，若AB=6cm，BC=10cm，则EC的长为考点：翻折变换（折叠问题）
专题：
分析：先求出BF、CF的长，利用勾股定理列出关于EF的方程，即可解决问题．
解答：解：如图，
∵四边形ABCD为矩形，
∴∠B=∠C=90°；
由题意得：AF=AD=10，ED=EF（设为λ），
则EC=6-λ；
由勾股定理得：BF2=AF2-AB2=64，
∴BF=8，CF=10-8=2；
由勾股定理得：λ2=22+（6-λ）2，
解得：λ=
，
∴EC=6-λ=
．
故答案为
．
解：如图，∵四边形ABCD为矩形，
∴∠B=∠C=90°；
由题意得：AF=AD=10，ED=EF（设为λ），
则EC=6-λ；
由勾股定理得：BF2=AF2-AB2=64，
∴BF=8，CF=10-8=2；
由勾股定理得：λ2=22+（6-λ）2，
解得：λ=
| 10 |
| 3 |
∴EC=6-λ=
| 8 |
| 3 |
故答案为
| 8 |
| 3 |
点评：该题主要考查了翻折变换及其应用问题；解题的关键是灵活运用勾股定理等几何知识来分析、判断、推理或解答．
练习册系列答案
相关题目
下列运算中，正确的是（ ）
| A、a•a2=a2 |
| B、（x+2）2=x2+4 |
| C、（ab3）2=ab6 |
| D、（-1）0=1 |
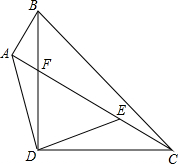如图，以Rt△ABC的斜边BC为斜边在△ABC的同侧作等腰Rt△BCD，连接AD，过D作DE⊥AD交AC于E，AB=1，AD=
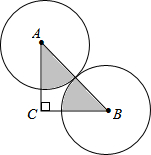如图，等腰Rt△ABC的斜边AB=10，⊙A，⊙B是等圆，求图中阴影部分的周长和面积．
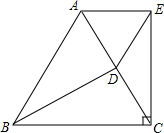如图，已知△ABC是等边三角形，D为边AC的中点，AE⊥EC，BD=EC．
如图，AB是半圆O的直径，OD平分弦BC于点F，且交半圆于点E．若∠AEC=∠ODB．