题目内容
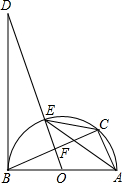 如图,AB是半圆O的直径,OD平分弦BC于点F,且交半圆于点E.若∠AEC=∠ODB.
如图,AB是半圆O的直径,OD平分弦BC于点F,且交半圆于点E.若∠AEC=∠ODB.(1)判断直线BD和半圆O的位置关系,并说明理由;
(2)当AB=26,BC=24时,求DF的长.
考点:切线的判定
专题:
分析:(1)根据垂径定理求得∠DFB=90°,根据同弧所对的圆周角相等,有∠AEC=∠ABC,又因为∠AEC=∠ODB,所以∠ABC=∠ODB,即∠ABC+∠BOD=90°,则有∠ODB+∠BOD=90°,即BD垂直于AB,所以BD为切线.
(2)由(1)可知OD⊥BC,∠ABC=∠ODB,所以有△BOD∽△FOB,而OF可由勾股定理求出,所以根据对应线段成比例求出DF的长.
(2)由(1)可知OD⊥BC,∠ABC=∠ODB,所以有△BOD∽△FOB,而OF可由勾股定理求出,所以根据对应线段成比例求出DF的长.
解答:解:(1)直线BD和半圆O相切;
∵OD平分BC,
∴OD⊥BC,
∴∠DFB=90°
∵∠AEC=∠ODB,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵∠ODB+∠DBC=90°
∴∠ABC+∠DBC=90°
∴∠ABD=90°
∴AB⊥BD
即直线BD和半圆O相切.
(2)∵OD⊥BC,BC=24,AB=26
∴BF=
BC=12,OB=13,
∴OF=
=5,
∵∠OBD=∠OFB=90°,∠BOD=∠FOB
∴△BOD∽△FOB,
∴
=
,
∴OD=
=
=
时,
∴DF=OD-OF=
,
∴DF的长为
.
∵OD平分BC,
∴OD⊥BC,
∴∠DFB=90°
∵∠AEC=∠ODB,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵∠ODB+∠DBC=90°
∴∠ABC+∠DBC=90°
∴∠ABD=90°
∴AB⊥BD
即直线BD和半圆O相切.
(2)∵OD⊥BC,BC=24,AB=26

∴BF=
| 1 |
| 2 |
∴OF=
| OB2-BF2 |
∵∠OBD=∠OFB=90°,∠BOD=∠FOB
∴△BOD∽△FOB,
∴
| BO |
| FO |
| OD |
| OB |
∴OD=
| OB2 |
| OF |
| 132 |
| 5 |
| 169 |
| 5 |
∴DF=OD-OF=
| 144 |
| 5 |
∴DF的长为
| 144 |
| 5 |
点评:此题主要考查了切线的判定,勾股定理的应用以及相似三角形的判定和性质,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
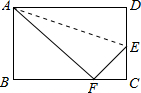 已知,如图,折叠长方形的一边AD使点D落在BC边的点F处,若AB=6cm,BC=10cm,则EC的长为
已知,如图,折叠长方形的一边AD使点D落在BC边的点F处,若AB=6cm,BC=10cm,则EC的长为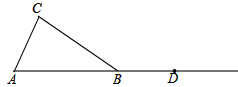 如图,在△ABC中,AB=BC,点D在AB的延长线上.
如图,在△ABC中,AB=BC,点D在AB的延长线上.