题目内容
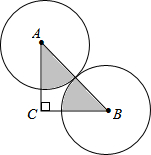 如图,等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,求图中阴影部分的周长和面积.
如图,等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,求图中阴影部分的周长和面积.考点:相切两圆的性质
专题:
分析:如图,将两个扇形组合为一个圆心角为90°的大扇形,运用有关面积或弧长公式,即可解决问题.
解答: 解:∵等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,
解:∵等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,
∴∠A=∠B=45°,圆的半径为5,
∴图中的两个扇形不重叠的放在一起,将构成一个半径为5,
圆心角为90°的扇形,
∴S阴影=
=
,阴影部分的周长=
+4×5=
+20,
即图中阴影部分的周长和面积分别为
+20、
.
 解:∵等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,
解:∵等腰Rt△ABC的斜边AB=10,⊙A,⊙B是等圆,∴∠A=∠B=45°,圆的半径为5,
∴图中的两个扇形不重叠的放在一起,将构成一个半径为5,
圆心角为90°的扇形,
∴S阴影=
| 90π•52 |
| 360 |
| 25π |
| 4 |
| 2π•5 |
| 4 |
| 5π |
| 2 |
即图中阴影部分的周长和面积分别为
| 5π |
| 2 |
| 25π |
| 4 |
点评:该题主要考查了相切两圆的性质及其应用问题;解题的关键是灵活运用扇形的面积公式和弧长公式来分析、判断、推理或解答;对变形转化能力、迁移引申能力等均提出了一定的要求.

练习册系列答案
相关题目
点P(-2,-1)关于y轴对称的点的坐标是( )
| A、(-2,-1) |
| B、(1,-2) |
| C、(2,-1) |
| D、(-1,-2) |
 某小区的一所健身中心的平面图如图所示,活动区是面积为200m2的钜形,其长为20m,餐饮区是一个半圆形,面积为πm2,休息区是一个三角形,试判断此三角形的形状,并说明理由.
某小区的一所健身中心的平面图如图所示,活动区是面积为200m2的钜形,其长为20m,餐饮区是一个半圆形,面积为πm2,休息区是一个三角形,试判断此三角形的形状,并说明理由. 如图,已知点C、D在线段AB上,若AC=
如图,已知点C、D在线段AB上,若AC=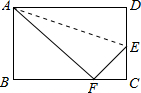 已知,如图,折叠长方形的一边AD使点D落在BC边的点F处,若AB=6cm,BC=10cm,则EC的长为
已知,如图,折叠长方形的一边AD使点D落在BC边的点F处,若AB=6cm,BC=10cm,则EC的长为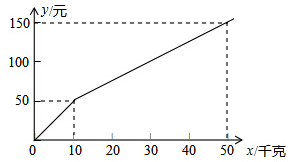 某种子公司以一定的价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不包含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(元)与一次购买种子数量x(千克)之间的函数关系如图所示
某种子公司以一定的价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不包含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(元)与一次购买种子数量x(千克)之间的函数关系如图所示