��Ŀ����
1����1���ⷽ����$\left\{\begin{array}{l}{3x-5y=3}\\{\frac{x}{2}-\frac{y}{3}=1}\end{array}\right.$����2����x��ֵ����x-15��2=169
��3�����㣺$\frac{1}{2}$+��-1��2009+$\sqrt{\frac{1}{4}}$-|-5|+$\sqrt{1\frac{9}{16}}$+$\root{3}{-2+\frac{3}{64}}$��
���� ��1���Ƚ��������еķ��̻�Ϊ������ĸ�ķ��̣����üӼ���Ԫ���������Ԫ����⼴�ɣ�
��2������ֱ�ӿ��������x��ֵ���ɣ�
��3���ȸ����������˷��������ķ��������������ٴ��������μ��㼴�ɣ�
��� �⣺��1��ԭ������ɻ�Ϊ$\left\{\begin{array}{l}3x-5y=3��\\ 3x-2y=6��\end{array}\right.$��
��-�ڵã�-3y=-3�����y=1����y=1����ٵã�3x-5=3�����x=$\frac{8}{3}$��
��ԭ������Ľ�Ϊ$\left\{\begin{array}{l}x=\frac{8}{3}\\ y=1\end{array}\right.$��
��2�����߿����ã�x-15=��13��
��x1=28��x2=2��
��3��ԭʽ=$\frac{1}{2}$-1+$\frac{1}{2}$-5+$\frac{5}{4}$-$\frac{5}{4}$
=-5��
���� ���⿼����ǽ��Ԫһ�η����飬��֪���Ԫһ�η�����ļӼ���Ԫ���ʹ�����Ԫ���ǽ�����Ĺؼ���

��ϰ��ϵ�д�
 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
�����Ŀ
12������ʽ���У���һԪһ�η��̵��ǣ�������
| A�� | x+1 | B�� | x+1=2 | C�� | x+y=1 | D�� | x2+1=2 |
9��ȥ����ʡ�滮�ؽ�У��Լ3876000ƽ���ף��������ȷ��ʮ��λ���ÿ�ѧ��������ʾΪ��������
| A�� | 3.8��106ƽ���� | B�� | 3.8��107ƽ���� | C�� | 3.9��106ƽ���� | D�� | 3.9��107ƽ���� |
16����ֱ֪������ϵ�У���P��x��y�����㣨5x+2y-12��2+|3x+2y-6|=0�����P����Ϊ��������
| A�� | ��3��-1.5�� | B�� | ��-3��-1.5�� | C�� | ��-2��-3�� | D�� | ��2��-3�� |
11�����������Ǽ�������ǣ�������
| A�� | ȫ�������εĶ�Ӧ����� | B�� | ����ʵ��a��b��c����a��b����ac2��bc2 | ||
| C�� | �����������Dz����ܶ������ | D�� | ��ֱ��a��b��c����a��b��b��c����a��c |
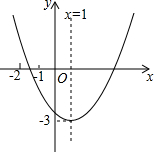 ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���������½��ۣ�
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���������½��ۣ� ��������������ͼ
��������������ͼ