Question

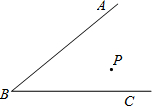如图，在∠ABC内有一点P，问：
（1）能否在BA、BC边上各找到一点M、N，使△PMN的周长最短？若能，请画图说明；若不能，说明理由．
（2）若∠ABC=40°，在（1）问的条件下，能否求出∠MPN的度数？若能，请求出它的数值；若不能，请说明原因．

Answer 1

分析：（1）分别作点P关于BA和BC的对称点P′和P′′，连接P′和P′′交BA和BC于M、N两点即可．
（2）在四边形BEPF中求出∠EPF的度数为140°，从而得出∠MPN+（∠MPP'+∠NPP''）=140°，∠MPN+（∠PMN+∠PNM）=∠MPN+2（∠MPP'+∠NPP''）=180°，解出即可得出答案．

解答：解：（1）能找到．
所作图形如下：
．
（2）∵∠ABC=40°，
∴∠EPF=140°，
∵MP=MP'，NP=NP''，
∴∠PMN=∠MP'P+∠MPP'=2∠MPP'，∠MNP=∠NPP''+∠NP''P=2∠NPP''
又∵∠MPN+（∠MPP'+∠NPP''）=140°，∠MPN+（∠PMN+∠PNM）=∠MPN+2（∠MPP'+∠NPP''）=180°，
∴（∠MPP'+∠NPP''）=40°，∠MPN=100°．

点评：本题考查了利用轴对称求解最短路径的知识，关键是掌握此类题题目解答的步骤，①找其中一点的对称点，②连接此对称点与另外一点．