题目内容
14.如图,在平面直角坐标系中,△ABC的顶点A(-3,0),B(0,3),点C在x轴上,AD⊥BC于D,交y轴于点E(0,1).(1)求点C的坐标;
(2)如图1,将线段CB绕点C顺时针旋转90°后得线段CF,连接BF.求△BCF的面积;
(3)在图2中,若∠APO=45°,求证:PA⊥PB.

分析 (1)根据△AOE≌△BOC得OE=OC即可求出点C坐标.
(2)先求出AE,根据BC=CF=AE即可求出△BCF面积.
(3)由∠APO=∠ABO=45°得A、P、B、O四点共圆,得到∠BPO=∠OAB=45°,即∠APB=∠APO+∠BPO=90°得到证明.
解答 (1)解:∵AD⊥BC,
∴∠EAO+∠BCO=90°,
∵∠CBO+∠BCO=90°,
∴∠EAO=∠CBO,
在△AOE或△BOC中,
$\left\{\begin{array}{l}{∠EAO=∠CBO}\\{AO=BO}\\{∠AOE=∠BOC=90°}\end{array}\right.$,
∴△AOE≌△BOC,
∴OE=OC=1,
∴点C坐标(1,0).
(2)∵△AOE≌△BOC,
∴BC=AE=$\sqrt{A{O}^{2}+E{O}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵BC=CF=$\sqrt{10}$,∠BCF=90°,
∴S△BCF=$\frac{1}{2}$BC•CF=$\frac{1}{2}$$•\sqrt{10}$$•\sqrt{10}$=5.
(3)∵OA=OB,∠AOB=90°,
∴∠ABO=∠BAO=45°,
∴∠APO=∠ABO=45°,
∴A、P、B、O四点共圆,
∴∠BPO=∠OAB=45°,
∴∠APB=∠APO+∠BPO=90°,
∴PA⊥PB.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、勾股定理、四点共圆以及有关圆的有关知识,寻找全等三角形是解决问题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
14.将点A(2,1)向下平移2个单位长度得到点A′,则点A′的坐标是( )
| A. | (0,1) | B. | (2,-1) | C. | (2,-2) | D. | (2,3) |
3.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了20次测试,测试成绩如下表(单位:环):
(1)根据表格中的数据,分别计算出甲、乙两人的平均成绩;
(2)你认为推荐谁参加省比赛更合适,请说明理由.
| 成绩(环) | 7 | 8 | 9 | 10 |
| 甲 | 3次 | 8次 | 5次 | 4次 |
| 乙 | 4次 | 6次 | 6次 | 4次 |
(2)你认为推荐谁参加省比赛更合适,请说明理由.

 如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向右B运动,到点B时停止运动,同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同,设点E的运动路程为x,△AEF的面积为y,求y与x的函数关系的函数关系式y=$\left\{\begin{array}{l}{2x(0≤x≤2)}\\{-12x2+3x(2<x≤4)}\end{array}\right.$,理由:三角形的面积公式.
如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向右B运动,到点B时停止运动,同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同,设点E的运动路程为x,△AEF的面积为y,求y与x的函数关系的函数关系式y=$\left\{\begin{array}{l}{2x(0≤x≤2)}\\{-12x2+3x(2<x≤4)}\end{array}\right.$,理由:三角形的面积公式.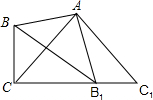 如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上.
如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上. 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠ADB=108度.
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠ADB=108度.