题目内容
17. 如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10cm,则⊙O的半径为( )
如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10cm,则⊙O的半径为( )| A. | 5cm | B. | 8cm | C. | 10cm | D. | 12cm |
分析 连接OC,根据切线的性质求出∠OCD=90°,求出∠ACO和∠A,求出∠COD,根据含30°角的直角三角形性质求出OD=2OC,即可得出答案.
解答 解:
连接OC,
∵CD切⊙O于点C,
∴∠OCD=90°,
∵∠ACD=120°,
∴∠ACO=30°,
∵OA=OC,
∴∠A=∠ACO=30°,
∴∠OCD=∠A+∠ACO=60°,
∴∠D=30°,
∴OD=2OC,
∵BD=10cm,
∴OC=OB=10cm,
即⊙O的半径为10cm,
故选C.
点评 本题考查了切线的性质,含30°角的直角三角形性质的应用,能求出OD=2OC是解此题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
相关题目
7.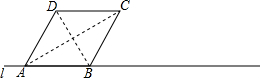 如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )
如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )
 如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )
如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )| A. | $\frac{8π}{3}$$+\frac{8\sqrt{3}π}{3}$ | B. | $\frac{16π}{3}$ | C. | $\frac{4π}{3}$+$\frac{4\sqrt{3}π}{3}$ | D. | $\frac{16\sqrt{3}π}{3}$ |
8.用配方法解一元二次方程x2-6x=-5的过程中,配方正确的是( )
| A. | (x+3)2=1 | B. | (x-3)2=1 | C. | (x+3)2=4 | D. | (x-3)2=4 |
5.某品牌商品,按标价八折出售,仍可获得10%的利润.若该商品标价为275元,则商品的进价为( )
| A. | 192.5元 | B. | 200元 | C. | 244.5元 | D. | 253元 |
12.某校组织1080名学生去外地参观,现有A、B两种不同型号的客车可供选择.在每辆车刚好满座的前提下,每辆B型客车比每辆A型客车多坐15人,单独选择B型客车比单独选择A型客车少租12辆,设A型客车每辆坐x人,根据题意列方程为( )
| A. | $\frac{1080}{x}=\frac{1080}{x-15}+12$ | B. | $\frac{1080}{x}=\frac{1080}{x-15}-12$ | ||
| C. | $\frac{1080}{x}=\frac{1080}{x+15}-12$ | D. | $\frac{1080}{x}=\frac{1080}{x+15}+12$ |
2.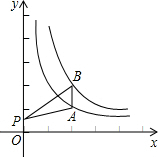 如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
 如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )| A. | 0.5 | B. | 1 | C. | 1.5 | D. | 2 |
6.如图,填在各方格中的三个数之间均具有相同的规律,据此规律,n的值是( )


| A. | 48 | B. | 56 | C. | 63 | D. | 74 |
7.一艘轮船从甲码头到乙码头顺水航行,用了2小时,从乙码头到甲码头逆水航行,用了2.5小时.已知水流速度为3千米/时.设轮船在静水中的速度为x千米/时,可列出的方程为( )
| A. | 2x+3=2.5x-3 | B. | 2(x+3)=2.5(x-3) | C. | 2x-3=2.5(x-3) | D. | 2(x-3)=2.5(x+3) |