题目内容
10.已知抛物线y=ax2-(3a+1)x+2(a+1)(a≠0),求证:无论a取何值,该抛物线与x轴都有两个交点.分析 令y=ax2-(3a+1)x+2(a+1)=0,求出根的判别式△,进而作出判断.
解答 证明:y=ax2-(3a+1)x+2(a+1)=0,
∵△=(3a+1)2-4a×2(a+1)=a2-2a+1=(a-1)2≥0,
∴无论a取何值,该抛物线与x轴都有两个交点.
点评 本题考查了抛物线与x轴的交点,△=b2-4ac决定抛物线与x轴的交点个数;△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
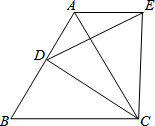 如图,点D是等边△ABC的边AB上的一动点,以CD为一边向上作等边△EDC,连接AE,请探究在点D的运动过程中,∠DAE的度数是否会发生变化?如果发生变化,请说明理由;如果不发生变化,请求出这个度数.
如图,点D是等边△ABC的边AB上的一动点,以CD为一边向上作等边△EDC,连接AE,请探究在点D的运动过程中,∠DAE的度数是否会发生变化?如果发生变化,请说明理由;如果不发生变化,请求出这个度数.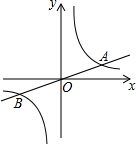 如图所示:已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A,B两点,且点A的横坐标为4
如图所示:已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A,B两点,且点A的横坐标为4 如图所示的几何体,共有4个面围成.
如图所示的几何体,共有4个面围成.