题目内容
a为何值时，适合条件
的点P（x，y）在第二象限？
|
考点：点的坐标,解二元一次方程组,解一元一次不等式组
专题：
分析：解方程组求出x、y，再根据第二象限内点的横坐标是负数，纵坐标是正数列出不等式组，然后求解即可．
解答：解：
，
①-②×2得，（a-8）y=-12，
解得y=
，
把y=
代入②得，x=
，
∵点P（x，y）在第二象限，
∴
，
解不等式②得，a＜8，
解不等式①得，a＞2，
所以，a的取值范围为2＜a＜8．
|
①-②×2得，（a-8）y=-12，
解得y=
| 12 |
| 8-a |
把y=
| 12 |
| 8-a |
| 16-8a |
| 8-a |
∵点P（x，y）在第二象限，
∴
|
解不等式②得，a＜8，
解不等式①得，a＞2，
所以，a的取值范围为2＜a＜8．
点评：本题考查了各象限内点的坐标的符号特征以及解不等式，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
练习册系列答案
相关题目
如图，⊙O是△ABC的外接圆，CD是AB边上的高，AE是⊙O的直径，求证：△AEC∽△CBD．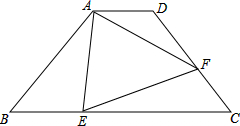
如图，等腰梯形ABCD中，AD∥BC，AD=2，AB=5，BC=8，点E在BC上，点F在CD上，且满足∠AEF=∠B，AF=EF，求BE的长．
2014年世界杯吉祥物“福来哥“来了，如图，他手中的三个气球上分别写有22°48′、18°54′、24°33′三个不同的角度，按要求解答下列问题：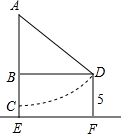
华夏古诗词源远流长，有许多古诗词与勾股定理有紧密联系，下面是明朝大数学家程大位所著的《直指算法统宗》里的一道题：