题目内容
4.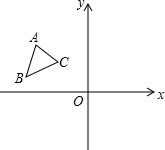 如图,△ABC中,A(-2,3),B(-3,1),C(-1,2).
如图,△ABC中,A(-2,3),B(-3,1),C(-1,2).(1)将△ABC向右平移3个单位长度,画出平移后的△A1B1C1;写出点A1的坐标(1,3).
(2)将△A1B1C1绕原点O顺时针旋转90°,画出旋转后的△A2B2C2;写出点C2的坐标(2,-2).
(3)直接写出经过两次变换后,线段BC运动到B2C2位置所扫过的部分的面积3+$\frac{7}{4}π$.
分析 (1)如图,利用点平移的规律分别写出点A、B、C的对应点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)如图,利用旋转的性质画出点A1、B1、C1的对应点A2、B2、C2,即可得到△A2B2C2,然后写出点C2的坐标;
(3)线段BC运动到B2C2位置所扫过的部分的面积分为平行四边形的面积和部分圆环的面积,而部分圆环的面积等于两扇形面积的差,于是可根据平行四边形的面积公式和扇形的面积公式求解.
解答 解:(1)如图,△A1B1C1为所作,点A1的坐标为(1,3);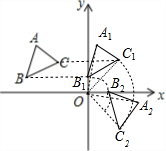
(2)如图,△A2B2C2为所作,点C2的坐标为(2,-2);
(3)OB1=1,OC1=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
所以线段BC运动到B2C2位置所扫过的部分的面积=3×1+$\frac{90•π•(2\sqrt{2})^{2}}{360}$-$\frac{90•π•{1}^{2}}{360}$=3+$\frac{7}{4}$π.
故答案为(1,3),(2,-2),3+$\frac{7}{4}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换和扇形的面积公式.

练习册系列答案
相关题目
 如图,△ABC的边AC与△BCD的边BD相交于点E,求证:AC+BD>AB+CD.
如图,△ABC的边AC与△BCD的边BD相交于点E,求证:AC+BD>AB+CD.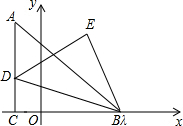 已知Rt△ABC中,∠ACB=90°,AC=BC,且点B(a+1,0),C(b,0)都在平面直角坐标系的x轴上,如图所示,且满足a2+b2-10a+4b+29=0,点D为射线AC上一动点且纵坐标为m,以BD为斜边,按顺时针顺序作△BDE,使∠DEB=90°,EB=ED.
已知Rt△ABC中,∠ACB=90°,AC=BC,且点B(a+1,0),C(b,0)都在平面直角坐标系的x轴上,如图所示,且满足a2+b2-10a+4b+29=0,点D为射线AC上一动点且纵坐标为m,以BD为斜边,按顺时针顺序作△BDE,使∠DEB=90°,EB=ED.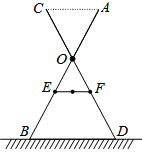 如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,求扣链EF与立杆AB的夹角∠OEF的度数.(精确到0.1°,可使用科学计算器)
如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,求扣链EF与立杆AB的夹角∠OEF的度数.(精确到0.1°,可使用科学计算器) 如图,O为四边形ABCD内的一点,且AO,DO分别平分∠BAD,∠ADC,已知∠B+∠C=150°,求∠AOD的度数.
如图,O为四边形ABCD内的一点,且AO,DO分别平分∠BAD,∠ADC,已知∠B+∠C=150°,求∠AOD的度数.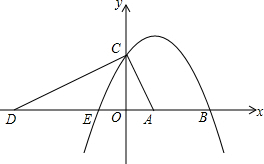 如图,抛物线y=ax2+bx+c(a<0)与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2,∠ACD=90°.
如图,抛物线y=ax2+bx+c(a<0)与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2,∠ACD=90°.