题目内容
19. 如图,一次函数y=-2x+4的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求:
如图,一次函数y=-2x+4的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求:(1)A、B、C三点的坐标.
(2)过B、C两点直线的解析式.
分析 (1)过点C作CD⊥x轴于D,如图,根据坐标轴上点的坐标特征求可确定A点和B点坐标,得到OA=2,OB=4,再利用“AAS”证明△ABO≌△CAD,得到AD=OB=4,CD=OA=2,于是得到C点坐标为(6,2);
(2)利用待定系数法求直线BC的解析式.
解答 解: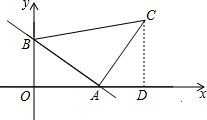 (1)过点C作CD⊥x轴于D,如图,
(1)过点C作CD⊥x轴于D,如图,
当y=0时,-2x+4=0,解得x=2,则A(2,0),OA=2,
当x=0时,y=-2x+4=4,则B(0,4),OB=4,
∵∠BAC=90°,
∴∠BAO+∠CAD=90°,
而∠BAO+∠ABO=90°,
∴∠ABO=∠CAD,
在△ABO和△CAD中,
$\left\{\begin{array}{l}{∠AOB=∠CDA}\\{∠ABO=∠CAD}\\{AB=CA}\end{array}\right.$,
∴△ABO≌△CAD,
∴AD=OB=4,CD=OA=2,
∴C点坐标为(6,2);
(2)设直线BC的解析式为y=kx+b,
把B(0,4),C(6,2)代入得$\left\{\begin{array}{l}{b=4}\\{6k+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=4}\end{array}\right.$,
故直线BC的解析式为y=-$\frac{1}{3}$x+4.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了待定系数法求一次函数解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.抛物线y=(x-1)2-3的顶点坐标是( )
| A. | (-1,-3) | B. | (-1,3) | C. | (1,-3) | D. | (1,3) |
10.下列各组数可能是一个三角形的边长的是( )
| A. | 1 2 4 | B. | 4 5 9 | C. | 4 6 8 | D. | 5 5 11 |
4.若-2am+4b4与5a2bn+1可以合并成一项,则mn的值是( )
| A. | -6 | B. | 8 | C. | -8 | D. | 9 |
11.下列图案是轴对称图形的有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.利用作角平分线的方法,可以把一个已知角( )
| A. | 三等分 | B. | 四等分 | C. | 五等分 | D. | 六等分 |