题目内容
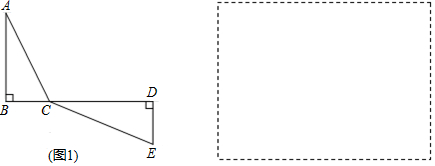
18.如图1,C为线段BD上一动点,分别过点B、D在BD两侧作AB⊥BD,ED⊥BD,连结AC,EC.
(1)如图1,已知AB=3,DE=2,BD=12,设CD=x.用含x的代数式表示AC+CE的长.(直接列式,不需化简)
(2))如图1,请问点C满足什么条件时,AC+CE的值最小?(直接写出结论,不需证明)
(3)根据以上的结论和规律,请在虚线框中构造图形,利用图形求出代数式$\sqrt{{x}^{2}+49}$+$\sqrt{(5-x)^{2}+25}$的最小值.
分析 (1)根据勾股定理直接列式;
(2)根据三角形的三边关系可得:当点C在直线AE上时,AC+CE的值最小,
(3)构建类似于图1的图3,作辅助线,构建直角△AEF,利用勾股定理求出AE的长,即代数式的最小值.
解答 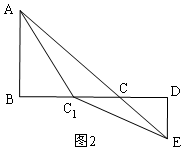 解:(1)∵CD=x,BD=12,
解:(1)∵CD=x,BD=12,
∴BC=12-x,
由勾股定理得:AC+CE=$\sqrt{{3}^{2}+(12-x)^{2}}+\sqrt{{2}^{2}+{x}^{2}}$;
(2)当点C在直线AE上时,如图2,AC+CE的值最小,
理由是:C1是线段BD上任意一点(C1不与C重合),
在△AC1E中,∵AC1+EC1>AE,
∴AC1+EC1>AC+CE,
即AC+CE的值最小,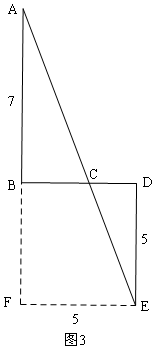
(3)如图3,线段BD,分别过点B、D在BD两侧作AB⊥BD,ED⊥BD,
已知AB=7,BD=DE=5,连结AE交BD于C,
由(2)得:此时AC+CE的值最小,
设BC=x,则CD=5-x,
∴AC+CE=$\sqrt{{x}^{2}+49}$+$\sqrt{(5-x)^{2}+25}$,
即代数式$\sqrt{{x}^{2}+49}$+$\sqrt{(5-x)^{2}+25}$的最小值就是线段AE的长,
过E作EF⊥AB,交AB的延长线于F,
∴∠F=90°,
∵AB⊥BD,ED⊥BD,
∴∠FBD=∠BDE=90°,
∴四边形EFBD是矩形,
∴EF=BD=5,BF=DE=5,
∴AF=5+7=12,
在Rt△AEF中,则勾股定理得:AE=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∴代数式$\sqrt{{x}^{2}+49}$+$\sqrt{(5-x)^{2}+25}$的最小值是13.
点评 本题考查了最短路径问题,正确确定C点的位置是解题的关键,本题还考查了两点之间线段最短或三角形的三边关系及勾股定理.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 如图所示,下列推理正确的个数有( )
如图所示,下列推理正确的个数有( )①若∠1=∠2,则AB∥CD
②若AD∥BC,则∠3+∠4
③若∠C+∠CDA=180°,则AD∥BC
④若AB∥CD,则∠C+∠CDA=180°.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | -3 | B. | -2 | C. | 0 | D. | 2 |
| A. | 1 | B. | 5 | C. | -1 | D. | -5 |