题目内容
10.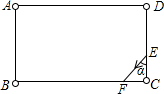 如图,矩形台球桌ABCD,其中A、B、C、D处有球洞,已知DE=4,CE=2,BC=6$\sqrt{3}$,球从E点出发,与DC夹角为α,经过BC、AB、AD三次反弹后回到E点,求tanα的取值范围( )
如图,矩形台球桌ABCD,其中A、B、C、D处有球洞,已知DE=4,CE=2,BC=6$\sqrt{3}$,球从E点出发,与DC夹角为α,经过BC、AB、AD三次反弹后回到E点,求tanα的取值范围( )| A. | $\sqrt{3}$≤tanα<$\frac{3}{2}$$\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{4}$<tanα<$\frac{3}{2}$$\sqrt{3}$ | C. | tanα=$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{4}$<tanα<3$\sqrt{3}$ |
分析 根据球的运动轨迹可知四个三角形相似,并且相对的两个三角形全等,由于DE=4,CE=2,可得CF=$\frac{1}{3}$BC,再根据正切的定义即可得到tanα的取值范围.
解答 解:如图: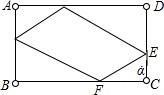
∵DE=4,CE=2,球从E点出发,与DC夹角为α,经过BC、AB、AD三次反弹后回到E点,
∴四个三角形相似,并且相对的两个三角形全等,
∴CF=$\frac{1}{1+2}$BC=2$\sqrt{3}$,
∴在Rt△CEP中,tanα=$\frac{CF}{CE}$=$\sqrt{3}$.
故选:C.
点评 考查了解直角三角形的应用,解题的关键是根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
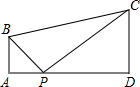 如图,四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=7,AB=2,DC=3,P为AD上一点,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,那么这样的点P有几个?为什么?
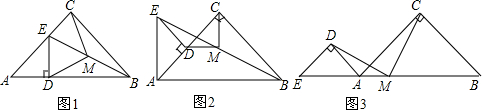
如图,四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=7,AB=2,DC=3,P为AD上一点,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,那么这样的点P有几个?为什么?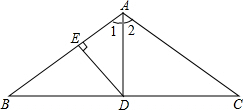 如图,在△ABC中,AB=AC,∠C=30°,D是BC边上中点,DE⊥AB于点E,BC=12,求:
如图,在△ABC中,AB=AC,∠C=30°,D是BC边上中点,DE⊥AB于点E,BC=12,求: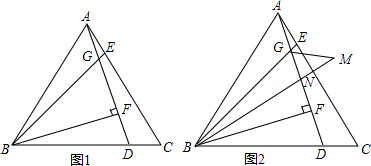

 如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.
如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.