题目内容
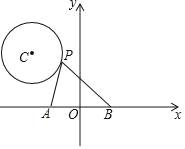
【题目】如图，在平面直角坐标系中，点P是以C（﹣
，
）为圆心，1为半径的⊙C上的一个动点，已知A（﹣1，0），B（1，0），连接PA，PB，则PA2+PB2的最小值是_____．
【答案】14﹣4
【解析】
设点P（x，y），表示出PA2+PB2的值，从而转化为求OP的最值，画出图形后可直观得出OP的最值，代入求解即可．
解：设P（x，y），
∵PA2＝（x+1）2+y2，PB2＝（x﹣1）2+y2，
∴PA2+PB2＝2x2+2y2+2＝2（x2+y2）+2，
∵OP2＝x2+y2，
∴PA2+PB2＝2OP2+2，
当点P处于OC与圆的交点上时，OP取得最值，
∴OP的最小值为CO-CP＝﹣1，
∴PA2+PB2最小值为14﹣4．
故答案是：14﹣4．
练习册系列答案
阅读快车系列答案
相关题目
