Question

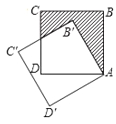
【题目】如图，边长为2的正方形绕点逆时针旋转得正方形.图中阴影部分的面积为__________．

Answer 1

【答案】

【解析】

设B′C′与CD的交点为E，连接AE，利用“HL”证明Rt△AB′E和Rt△ADE全等，根据全等三角形对应角相等∠DAE＝∠B′AE，再根据旋转角求出∠DAB′＝60°，然后求出∠DAE＝30°，再解直角三角形求出DE，然后根据阴影部分的面积＝正方形ABCD的面积四边形ADEB′的面积，列式计算即可得解．

解：如图，设B′C′与CD的交点为E，连接AE，

在Rt△AB′E和Rt△ADE中，

∵，

∴Rt△AB′E≌Rt△ADE（HL），

∴∠DAE＝∠B′AE，

∵旋转角为30°，

∴∠DAB′＝60°，

∴∠DAE＝×60°＝30°，

∴DE＝2×tan30°=2×＝，

∴阴影部分的面积＝2×22×（×）＝．

故填：.