题目内容
 如图,在△ABC中,AB=AC,D、E分别是边BC、AC上的一点,且BD=EC,∠ADE=∠B,若∠ADE=x°,求∠ADB的度数.
如图,在△ABC中,AB=AC,D、E分别是边BC、AC上的一点,且BD=EC,∠ADE=∠B,若∠ADE=x°,求∠ADB的度数.考点:全等三角形的判定与性质
专题:
分析:由条件可知∠BAD=∠CDE,可证得△ABD≌△DCE,可得∠ADB=∠CEC,DE=AD,利用三角形内角和可表示出∠ADE,进一步可求得∠ADB.
解答:解:∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B,∠ADE+∠EDC=∠B+∠BAD,
∴∠BAD=∠EDC,
在△ABD和△DCE中,
,
∴△ABD≌△DCE(AAS),
∴∠ADB=∠DEC,DE=AD,
∴∠DAE=∠DEA,且∠ADE=x°,
∴∠DAE=
(180°-x),
∴∠DEC=∠ADE+∠DAE=x°+
(180°-x°)=90°+
x°,
∴∠ADB=90°+
x°.
∴∠B=∠C,
∵∠ADE=∠B,∠ADE+∠EDC=∠B+∠BAD,
∴∠BAD=∠EDC,
在△ABD和△DCE中,
|
∴△ABD≌△DCE(AAS),
∴∠ADB=∠DEC,DE=AD,
∴∠DAE=∠DEA,且∠ADE=x°,
∴∠DAE=
| 1 |
| 2 |
∴∠DEC=∠ADE+∠DAE=x°+
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADB=90°+
| 1 |
| 2 |
点评:本题主要考查全等三角形的判定及等腰三角形的性质,由条件得到∠ADB=∠DEC是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若草坪部分总面积为112m2,设小路宽为xm,那么x满足的方程是( )
如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若草坪部分总面积为112m2,设小路宽为xm,那么x满足的方程是( )| A、2x2-25x+16=0 |
| B、x2-25x+32=0 |
| C、x2-17x+16=0 |
| D、x2-17x-16=0 |
用配方法解方程x2+10x+11=0,变形后的结果正确的是( )
| A、(x+5)2=-11 |
| B、(x+5)2=11 |
| C、(x+5)2=14 |
| D、(x+5)2=-14 |
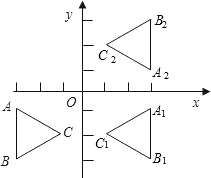 如图,直角坐标系中,△ABC为等边三角形,其中A、B、C的坐标分别为(-3,-1),(-3,-3),(-3+
如图,直角坐标系中,△ABC为等边三角形,其中A、B、C的坐标分别为(-3,-1),(-3,-3),(-3+