题目内容
已知a、b是不为零的实数,对于任意实数x、y,都有(a2+b2)(x2+y2)+8bx+8ay-k2+k+28≥0,其中k是实数,则k的最大值为多少?
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:根据配方,可得[x+
]2+[y+
]2-
≥0,根据非负数的和为非负数,可得-
≥0,根据分式的性质,可得不等式组,根据解不等式组,可得答案.
| 4b |
| a2+b2 |
| 4a |
| a2+b2 |
| k2-k-12 |
| a2+b2 |
| k2-k-12 |
| a2+b2 |
解答:解:对任意实数x,y,都有(a2+b2)(x2+y2)+8bx+8ay-k2+k+28≥0,
两边都除以(a2+b2),得x2+
+y2+
-
≥0
分别配方:
[x+
]2+[y+
]2-
≥0.
若不等式恒成立,需
k2-k-12≤0.
因式分解,得
(k-4)(k+3)≤0,
解得-3≤k≤4,
k的最大值为4.
两边都除以(a2+b2),得x2+
| 8bx |
| a2+b2 |
| 8ay |
| a2+b2 |
| k2-k-28 |
| a2+b2 |
分别配方:
[x+
| 4b |
| a2+b2 |
| 4a |
| a2+b2 |
| k2-k-12 |
| a2+b2 |
若不等式恒成立,需
k2-k-12≤0.
因式分解,得
(k-4)(k+3)≤0,
解得-3≤k≤4,
k的最大值为4.
点评:本题考查了配方法的应用,配方是解题关键,利用因式分解解不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知∠A=45°15′,∠B=45°12′18″,∠C=45.15°,则( )
| A、∠A>∠B>∠C |
| B、∠B>∠A>∠C |
| C、∠A>∠C>∠B |
| D、∠C>∠A>∠B |
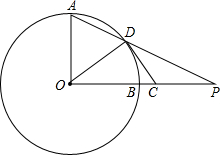 如图,半径OA⊥OB,P是OB延长线上一点,PA交⊙O于D,过D作⊙O的切线CE交PO于C点,求证:PC=CD.
如图,半径OA⊥OB,P是OB延长线上一点,PA交⊙O于D,过D作⊙O的切线CE交PO于C点,求证:PC=CD. 如图,直线AB、CD相交于点O,OE、OF分别是平角∠AOB和平角∠COD的平分线,写出图中的锐角为
如图,直线AB、CD相交于点O,OE、OF分别是平角∠AOB和平角∠COD的平分线,写出图中的锐角为 如图,求sinA和sinB的值.
如图,求sinA和sinB的值.