题目内容
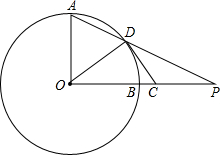 如图,半径OA⊥OB,P是OB延长线上一点,PA交⊙O于D,过D作⊙O的切线CE交PO于C点,求证:PC=CD.
如图,半径OA⊥OB,P是OB延长线上一点,PA交⊙O于D,过D作⊙O的切线CE交PO于C点,求证:PC=CD.考点:切线的性质
专题:证明题
分析:先根据切线的性质,由CD为⊙O的切线得到∠ODC=90°,则∠ADO+∠PDC=90°,加上∠ADO=∠A,所以∠A+∠PDC=90°,再利用OA⊥OB得到∠A+∠P=90°,于是有∠PDC=∠P,然后根据等腰三角形的判定定理得PC=CD.
解答:证明:∵CD为⊙O的切线,
∴∠ODC=90°,
∴∠ADO+∠PDC=90°,
而OA=OD,
∴∠ADO=∠A,
∴∠A+∠PDC=90°,
∵OA⊥OB,
∴∠A+∠P=90°,
∴∠PDC=∠P,
∴PC=CD.
∴∠ODC=90°,
∴∠ADO+∠PDC=90°,
而OA=OD,
∴∠ADO=∠A,
∴∠A+∠PDC=90°,
∵OA⊥OB,
∴∠A+∠P=90°,
∴∠PDC=∠P,
∴PC=CD.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了等腰三角形的判定定理.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
下列各式中正确的是( )
A、1÷
| ||
| B、0-(-5)=-5 | ||
| C、-6-|-6|=0 | ||
| D、5-(+6)=-1 |
在一幅长90cm,宽40cm的风景画的四周外围镶上一条宽度相同的金色纸边,制成一幅挂图,如果要求风景画的面积是整个挂图的80%.若设金色纸边的宽为xcm.根据题意列方程,并整理得( )
| A、x2-65x+350=0 |
| B、x2+65x-350=0 |
| C、x2+65x-225=0 |
| D、x2-65x+225=0 |
 如图,四边形ABCD内接于⊙O,∠B=50°,∠ACD=25°,∠BAD=65°,求证:
如图,四边形ABCD内接于⊙O,∠B=50°,∠ACD=25°,∠BAD=65°,求证: