题目内容
20.某试卷共有30道题,每道题选对得10分,选错了或者不选扣5分,至少要选对16道题,其得分才能不少于80分.分析 根据选对的题的数目乘以每道题选对的得分可求得其选对题的总分数,同理求出选错或不选的总分数,根据题意可列不等式求解.
解答 解:设应选对x道题,则选错或不选的题数有(30-x),根据其得分不少于80分得:10x-5(30-x)≥80
得:x≥$\frac{46}{3}$
在本题中x应为正整数且不能超过20,故至少应选对16道题.
故答案是:16.
点评 本题考查了一元一次不等式的应用.用不等式解应用问题时,要注意未知数的限制条件,在本题中应是正整数.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
10.解方程:$\frac{x}{3}=1-\frac{x-1}{4}$去分母后正确的是( )
| A. | 4x=1-3(x-1) | B. | x=1-(x-1) | C. | 4x=3-(x-1) | D. | 4x=12-3(x-1) |
11.若分式$\frac{2x-y}{y}$中的x,y的值变为原来的2倍,则此分式的值( )
| A. | 不变 | B. | 发生变化 | C. | 是原来的2倍 | D. | 是原来的$\frac{1}{2}$ |
15. 如图所示的解集,正确的是( )
如图所示的解集,正确的是( )
 如图所示的解集,正确的是( )
如图所示的解集,正确的是( )| A. | x<-2 | B. | x≤-2 | C. | x>-2 | D. | x≥-2 |
5.在平面直角坐标系中,已知点P的坐标为(5,12),则OP的长为( )
| A. | 5 | B. | 12 | C. | 13 | D. | 14 |
 如图,在小正方形边长均为单位1的方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
如图,在小正方形边长均为单位1的方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.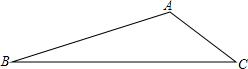 △ABC是武汉市在拆除违章建筑后的一块三角形空地,已知∠A=150°,AB=30m,AC=20m,如果要在这块空地上种草皮,按每平方米a元计算,则需要资金多少元?
△ABC是武汉市在拆除违章建筑后的一块三角形空地,已知∠A=150°,AB=30m,AC=20m,如果要在这块空地上种草皮,按每平方米a元计算,则需要资金多少元?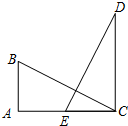 如图,AB⊥AC,垂足为A,CD⊥AC,垂足为C,DE⊥BC,且AB=CE,若BC=5cm,则DE的长为5cm.
如图,AB⊥AC,垂足为A,CD⊥AC,垂足为C,DE⊥BC,且AB=CE,若BC=5cm,则DE的长为5cm.