题目内容
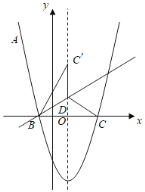
【题目】已知二次函数解析式为y=mx2﹣2mx+m﹣![]() ,二次函数与x轴交于A、B两点(B在A右侧),与y轴交于C点,二次函数顶点为M.已知∠OMB=90°.
,二次函数与x轴交于A、B两点(B在A右侧),与y轴交于C点,二次函数顶点为M.已知∠OMB=90°.
①求顶点坐标.
②求二次函数解析式.
③N为线段BM中点,在二次函数的对称轴上是否存在一点P,使得∠PON=60°,若存在求出点P坐标,若不存在,请说明理由.
【答案】①顶点M(1,﹣![]() );②y
);②y![]() ;③存在,当点P(1,
;③存在,当点P(1,![]() )或(1,﹣3
)或(1,﹣3![]() )时,使得∠PON=60°.
)时,使得∠PON=60°.
【解析】
①先求出对称轴为x=1,代入解析式可求顶点坐标;
②通过证明△MEO∽△BEM,可得![]() ,可求BE=3,可得点B坐标,代入可求解析式;
,可求BE=3,可得点B坐标,代入可求解析式;
③分两种情况讨论,由相似三角形的性质和两点距离公式可求解.
①∵x=﹣![]() =1,
=1,
∴y=m﹣2m+m﹣![]() =﹣
=﹣![]() ,
,
∴顶点M(1,﹣![]() );
);
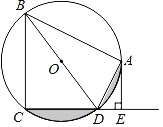
②如图1,过点M作ME⊥OB于E,
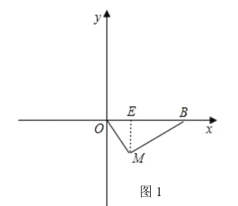
∵顶点M(1,﹣![]() )
)
∴EM=![]() ,OE=1,
,OE=1,
∵∠OMB=90°.
∴∠OME+∠BME=90°,
∵ME⊥OB,
∴∠OME+∠MOE=90°,
∴∠MOE=∠EMB,且∠MEO=∠MEB=90°,
∴△MEO∽△BEM,
∴![]() ,
,
∴BE=3,
∴OB=OE+BE=4,
∴点B(4,0),
∴0=16m﹣8m+m﹣![]() ,
,
∴m=![]() ,
,
∴二次函数解析式为:y![]() ;
;
③如图2,若点P在x轴上方,
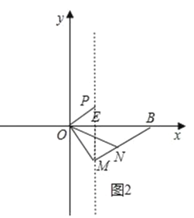
∵顶点M(1,﹣![]() )
)
∴EM=![]() ,OE=1,
,OE=1,
∴tan∠EOM=![]() =
=![]() ,OM=
,OM=![]() =
=![]() =2,
=2,
∴∠EOM=60°,
又∵∠OMB=90°
∴MB=OM![]() tan∠EOM=2
tan∠EOM=2![]() ,
,
∵N为线段BM中点,
∴MN=![]() ,
,
∵∠PON=∠MOB=60°,
∴∠POE=∠OMN,且∠PEO=∠OMN=90°,
∴△OMN∽△OEP,
∴![]() ,
,
∴PE=![]() ,
,
∴点P(1,![]() );
);
如图3,若点P在x轴下方,在OP上截取OF=ON,连接NF,
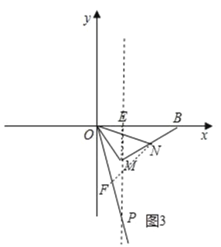
∵OM=2,MN=![]() ,
,
∴ON=![]()
∵ON=OF,∠PON=60°,
∴△ONF是等边三角形,
∴OF=ON=FN=![]() ,
,
∵N为线段BM中点,点B(4,0),点M(1,﹣![]() )
)
∴点N(![]() ,﹣
,﹣![]() )
)
设点F(a,b)
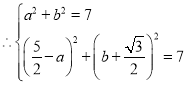
解得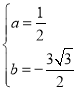
∴点F(![]() ,
,![]() )
)
∴直线OF的解析式为:y=﹣3![]() x,
x,
∴当x=1时,y=﹣3![]() ,
,
∴点P(1,﹣3![]() )
)
综上所述:当点P(1,![]() )或(1,﹣3
)或(1,﹣3![]() )时,使得∠PON=60°.
)时,使得∠PON=60°.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案