题目内容
17.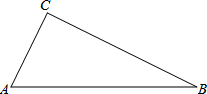 如图,在Rt△ABC中,∠ACB=90°,AC=1,AB=2
如图,在Rt△ABC中,∠ACB=90°,AC=1,AB=2(1)求作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)所作的圆中,求出劣弧$\widehat{BC}$的长l.
分析 (1)使以O为圆心的圆经过A、B、C三点,即做三角形的外接圆,因为△ABC为直角三角形,所以作斜边的中点,以该点为圆心OA为半径作圆即可;
(2)由,∠ACB=90°,AC=1,AB=2,易得∠B=30°,∠A=60°,∠BOC=120°,由弧长计算公式得出结论.
解答 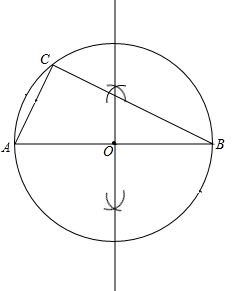 解:(1)如图所示,⊙O即为所求;
解:(1)如图所示,⊙O即为所求;
(2)∵AC=1,AB=2,
∴∠B=30°,∠A=60°,
∴∠BOC=120°,
∴l=$\frac{120°π•1}{180°}$=$\frac{2π}{3}$
点评 本题主要考查了三角形外接圆的做法,含30°直角三角形的性质及弧长的计算,数形结合,掌握直角三角形的性质是解答此题的关键.

练习册系列答案
相关题目
5.一个多边形的内角和是360°,这个多边形是( )
| A. | 三角形 | B. | 四边形 | C. | 六边形 | D. | 不能确定 |
2.某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩$\overline{x}$及其方差s2如表所示,如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| s2 | 1 | 1 | 1.2 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
6.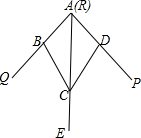 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
12.三角形三边长为6、8、10,那么最长边上的高为( )
| A. | 6 | B. | 4.5 | C. | 4.8 | D. | 8 |
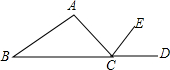 如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是60度.
如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是60度. 如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是90°.
如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是90°.