题目内容
12. 如图,矩形ABCD,AB=2,BC=1,将矩形ABCD绕点A顺时针旋转90°得矩形AEFG,连接CG、EG,则∠CGE=45°.
如图,矩形ABCD,AB=2,BC=1,将矩形ABCD绕点A顺时针旋转90°得矩形AEFG,连接CG、EG,则∠CGE=45°.
分析 连接CE,可证得△CDE≌△GFE,可求得△CEG为等腰直角三角形,可求得答案.
解答 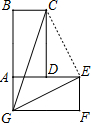 解:
解:
如图,连接CE,
∵AB=2,BC=1,
∴DE=EF=1,CD=GF=2,
在△CDE和△GFE中
$\left\{\begin{array}{l}{CD=GF}\\{∠CDE=∠GFE}\\{DE=EF}\end{array}\right.$
∴△CDE≌△GFE(SAS),
∴CE=GE,∠CED=∠GEF,
∵∠AEG+∠GEF=90°,
∴∠CEG=∠AEG+∠CED=90°,
∴∠CGE=45°,
故答案为:45°.
点评 本题主要考查矩形和性质和全等三角形的判定和性质,由条件证得△CGE为等腰直角三角形是解题的关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
2.下列等式计算正确的是( )
| A. | (-2)+3=-1 | B. | 3-(-2)=1 | C. | (-3)+(-2)=6 | D. | (-3)+(-2)=-5 |
20.若(x-y+3)2+|2x+y|=0,则xy的值为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
1.计算4+(-6)的结果等于( )
| A. | -2 | B. | 2 | C. | 10 | D. | -10 |
2.关于x的方程x2+6x+a=0的左边是完全平方式,则a的值为( )
| A. | 9 | B. | 12 | C. | 36 | D. | 144 |
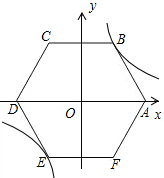 如图,在平面直角坐标系中,正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=$\frac{9\sqrt{3}}{x}$位于第一象限的图象上,则正六边形ABCDEF的边长为6.
如图,在平面直角坐标系中,正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=$\frac{9\sqrt{3}}{x}$位于第一象限的图象上,则正六边形ABCDEF的边长为6.