题目内容
用适当的方法解下列方程
(1)x2+12x+27=0
(2)2x+6=(x+3)2
(3)5x+2=3x2
(4)(3x+5)2-4(3x+5)+3=0.
(1)x2+12x+27=0
(2)2x+6=(x+3)2
(3)5x+2=3x2
(4)(3x+5)2-4(3x+5)+3=0.
考点:解一元二次方程-因式分解法
专题:
分析:(1)用因式分解法解答即可;
(2)先化成一般形式,然后用因式分解法解答即可;
(3)先整理成一般形式,然后用因式分解法解答即可;
(4)将(3x+5)看成一个整体,然后用因式分解法解答即可.
(2)先化成一般形式,然后用因式分解法解答即可;
(3)先整理成一般形式,然后用因式分解法解答即可;
(4)将(3x+5)看成一个整体,然后用因式分解法解答即可.
解答:
解:(1)x2+12x+27=0,
(x+3)(x+9)=0
x+3=0或x+9=0,
∴x1=-3,x2=-9;
(2)2x+6=(x+3)2
整理成一般形式:
x2+4x+3=0,
(x+1)(x+3)=0,
x+1=0或x+3=0,
∴x1=-1,x2=-3;
(3)5x+2=3x2
整理成一般形式:
3x2-5x-2=0,
(x-2)(3x-1)=0,
x-2=0或3x-1=0,
∴x1=2,x2=
;
(4)(3x+5)2-4(3x+5)+3=0.
(3x+5-1)(3x+5-3)=0,
3x+5-1=0或3x+5-3=0,
∴x1=-
,x2=-
.
(x+3)(x+9)=0
x+3=0或x+9=0,
∴x1=-3,x2=-9;
(2)2x+6=(x+3)2
整理成一般形式:
x2+4x+3=0,
(x+1)(x+3)=0,
x+1=0或x+3=0,
∴x1=-1,x2=-3;
(3)5x+2=3x2
整理成一般形式:
3x2-5x-2=0,
(x-2)(3x-1)=0,
x-2=0或3x-1=0,
∴x1=2,x2=
| 1 |
| 3 |
(4)(3x+5)2-4(3x+5)+3=0.
(3x+5-1)(3x+5-3)=0,
3x+5-1=0或3x+5-3=0,
∴x1=-
| 4 |
| 3 |
| 2 |
| 3 |
点评:本题考查了用因式分解法解一元二次方程,解(4)的关键是:将(3x+5)看成一个整体.

练习册系列答案
相关题目
不改变分式
的值,把它的分子和分母中的各项都化为整数,则所得的结果为( )
| 0.3x-1 | ||
x+
|
A、
| ||
B、
| ||
C、
| ||
D、
|
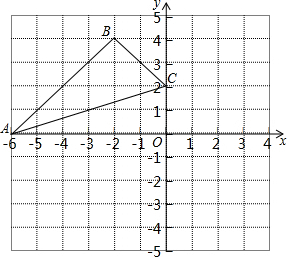 如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件:
如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件: 如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们的测量数据计算这棵树的高度.
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们的测量数据计算这棵树的高度. 如图,?ABCD中,E是AD的中点,连接CE并延长,与BA的延长线交于点F. 请你找出图中与AF相等的一条线段,并加以证明.(不再添加其它线段,不再标注或使用其它字母)
如图,?ABCD中,E是AD的中点,连接CE并延长,与BA的延长线交于点F. 请你找出图中与AF相等的一条线段,并加以证明.(不再添加其它线段,不再标注或使用其它字母)