题目内容
阅读材料,并解答下列问题:(x-1)(x+1)=x2-1;(x-1)(x2+x+1)=x3-1;(x-1)(x3+x2+x+1)=x4-1,…
(1)试求26+25+24+23+22+2+1的值.
(2)判断22014+22013+22012+…+22+2+1的结果的个位数字是几.
(1)试求26+25+24+23+22+2+1的值.
(2)判断22014+22013+22012+…+22+2+1的结果的个位数字是几.
考点:平方差公式,尾数特征
专题:规律型
分析:(1)根据题中的规律将原式变形后,计算即可得到结果;
(2)根据题中的规律将原式变形后,计算得到结果,即可确定出个位数字.
(2)根据题中的规律将原式变形后,计算得到结果,即可确定出个位数字.
解答:解:(1)原式=(2-1)(26+25+24+23+22+2+1)=27-1;
(2)原式=(2-1)(22014+22013+22012+…+22+2+1)=22015-1,
21=2,22=4,23=8,24=16,依次循环,
∵2015÷4=503…3,
∴22015个位数为8,
则结果个位数为7.
(2)原式=(2-1)(22014+22013+22012+…+22+2+1)=22015-1,
21=2,22=4,23=8,24=16,依次循环,
∵2015÷4=503…3,
∴22015个位数为8,
则结果个位数为7.
点评:此题考查了平方差公式,弄清题中的规律是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知4x2-mx+25是完全平方式,则常数m的值为( )
| A、10 | B、±10 |
| C、-20 | D、±20 |
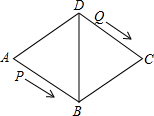 如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.
如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.