题目内容
19.已知一次函数y1=-$\frac{2}{3}$x+$\frac{2}{3}$a,y2=$\frac{3}{2}$x-$\frac{a-1}{2}$,试求当a为何值时,两函数图象的交点在第二象限?分析 根据两直线相交的问题,通过解方程组$\left\{\begin{array}{l}{y=-\frac{2}{3}x+\frac{2}{3}a}\\{y=\frac{3}{2}x-\frac{a-1}{2}}\end{array}\right.$得两函数的交点坐标,再利用第二象限点的坐标特征得到$\left\{\begin{array}{l}{\frac{7a-3}{13}<0}\\{\frac{89a+12}{78}>0}\end{array}\right.$,然后解不等式组即可.
解答 解:解方程组$\left\{\begin{array}{l}{y=-\frac{2}{3}x+\frac{2}{3}a}\\{y=\frac{3}{2}x-\frac{a-1}{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{7a-3}{13}}\\{y=\frac{89a+12}{78}}\end{array}\right.$,则两函数的交点坐标为($\frac{7a-3}{13}$,$\frac{89a+12}{78}$),
当$\left\{\begin{array}{l}{\frac{7a-3}{13}<0}\\{\frac{89a+12}{78}>0}\end{array}\right.$时,两函数图象的交点在第二象限,
解得-$\frac{12}{89}$<a<$\frac{3}{7}$.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
7.如图,所给图形中是中心对称图形但不是轴对称图形的是( )
| A. | 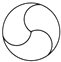 | B. | 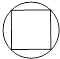 | C. |  | D. | 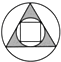 |
4.下列各整式中,次数为5次的单项式是( )
| A. | xy4 | B. | xy5 | C. | x+y4 | D. | x+y5 |
8.对一组数据:1,-2,4,2,5的描述正确的是( )
| A. | 中位数是4 | B. | 众数是2 | C. | 平均数是2 | D. | 方差是7 |
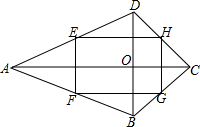 如图,在四边形ABCD中,AC⊥DB,垂足为O,点E、F、G、H分别为AD、AB、BC、CD的中点,求证:四边形EFGH是矩形.
如图,在四边形ABCD中,AC⊥DB,垂足为O,点E、F、G、H分别为AD、AB、BC、CD的中点,求证:四边形EFGH是矩形. 用一根长为a m的篱笆在空地上围一绿化场地,现有两种方案:
用一根长为a m的篱笆在空地上围一绿化场地,现有两种方案: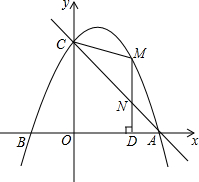 如图,二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过点A,B(-2,0),C(0,4),作直线AC,点M是二次函数图象上的一动点,过点作MD⊥x轴,垂足为点D,交直线AC于点N,连结CM.
如图,二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过点A,B(-2,0),C(0,4),作直线AC,点M是二次函数图象上的一动点,过点作MD⊥x轴,垂足为点D,交直线AC于点N,连结CM.