题目内容
13.如果abc>0,则$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$=-1或3.分析 abc>0,可知a、b、c中二负一正或都是正,再分四种情况讨论即可解答.
解答 解:∵abc>0,
∴a、b、c中二负一正,或都是正,
当a、b为负数,c为正数时,原式=-1-1+1=-1;
当a、c为负数,b为正数时,原式=-1+1-1=-1;
当b、c为负数,a为正数时,原式=1-1-1=-1;
当a、b、c都是正数时,原式=1+1+1=3.
故答案为:-1或3.
点评 本题考查了绝对值的知识,解题的关键是判断a、b、c的符号,再分类讨论.此题难度不大,易于掌握.

练习册系列答案
相关题目
4.下列说法不正确的是( )
| A. | $\frac{1}{25}$的平方根是$±\frac{1}{5}$ | B. | $\root{3}{-27}$=-3 | ||
| C. | (-0.1)2的平方根是±0.1 | D. | $\sqrt{81}$的平方根±9 |
3.下列几何体中,属于锥体的有( )
| A. |  | B. |  | C. |  | D. |  |

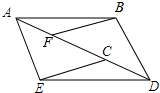 如图,AB∥ED,点F、C在AD上,AB=DE,AF=DC,试说明BC=EF.
如图,AB∥ED,点F、C在AD上,AB=DE,AF=DC,试说明BC=EF.