题目内容
8.用适当的方法解方程(1)(x+2)2-8=0;
(2)x(x-3)=x;
(3)x2+5x-4=0;
(4)$\frac{(x-1)^{2}}{{x}^{2}}$-$\frac{x-1}{x}$-2=0.
分析 (1)先将-8移到方程的右边,再利用直接开平方法求解;
(2)先移项,使方程的右边为零,再利用因式分解法求解;
(3)利用公式法求解;
(4)设$\frac{x-1}{x}$=y,则原方程变形为y2-y-2=0,先求y,再求x即可.
解答 解:(1)(x+2)2-8=0,
(x+2)2=8,
x+2=±2$\sqrt{2}$,
x1=-2+2$\sqrt{2}$,x2=-2-2$\sqrt{2}$;
(2)x(x-3)=x,
x(x-3)-x=0,
x(x-3-1)=0,
x=0,或x-4=0,
x1=0,x2=4;
(3)x2+5x-4=0,
∵△=25-4×1×(-4)=41>0,
∴x=$\frac{-5±\sqrt{41}}{2}$,
x1=$\frac{-5+\sqrt{41}}{2}$,x2=$\frac{-5-\sqrt{41}}{2}$;
(4)$\frac{(x-1)^{2}}{{x}^{2}}$-$\frac{x-1}{x}$-2=0.
设$\frac{x-1}{x}$=y,则原方程变形为y2-y-2=0,
解得y1=2,y2=-1.
当y1=2时,$\frac{x-1}{x}$=2,解得x1=-1;
当y2=-1时,$\frac{x-1}{x}$=-1,解得x=$\frac{1}{2}$.
经检验x1=-1,x2=$\frac{1}{2}$都是原方程的根.
所以原方程的根是x1=-1,x2=$\frac{1}{2}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
20.下列几对数中,互为相反数的是( )
| A. | $\frac{3}{4}$和-0.75 | B. | -5和﹢3 | C. | $\frac{1}{3}$和0.3 | D. | $\frac{1}{2}$和-2 |
17.有两根长度分别为5cm和8cm的木棒,若不改变木棒的长度钉成一个三角形木架,则另一根木棒应选( )
| A. | 3cm | B. | 5cm | C. | 13cm | D. | 20cm |
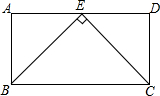 如图,在矩形ABCD中,E是AD的中点,连接BE,CE,且BE⊥CE.若矩形的周长为18cm,求矩形各边的长.
如图,在矩形ABCD中,E是AD的中点,连接BE,CE,且BE⊥CE.若矩形的周长为18cm,求矩形各边的长.