Question

17．如图，点B、C、D都在⊙O上，过C点作CA∥BD交OD的延长线于点A，连接BC，∠B=∠A=30°，BD=4$\sqrt{3}$．
（1）求证：AC是⊙O的切线；
（2）求由线段AC、AD与弧$\widehat{CD}$所围成的阴影部分的面积．（结果保留π）

Answer 1

分析 （1）连接OC，根据圆周角定理求出∠COA，根据三角形内角和定理求出∠OCA，根据切线的判定推出即可；
（2）求出DE，解直角三角形求出OC，分别求出△ACO的面积和扇形COD的面积，即可得出答案．

解答 （1）证明：连接OC，交BD于E，
∵∠B=30°，∠B=$\frac{1}{2}$∠COD，
∴∠COD=60°，
∵∠A=30°，
∴∠OCA=90°，
即OC⊥AC，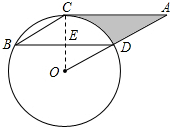
∴AC是⊙O的切线；

（2）解：∵AC∥BD，∠OCA=90°，BD=4$\sqrt{3}$，
∴∠OED=∠OCA=90°，
∴DE=$\frac{1}{2}$BD=2$\sqrt{3}$，
∵sin∠COD=$\frac{DE}{OD}$，
∴OD=4，
在Rt△ACO中，tan∠COA=$\frac{AC}{OC}$，
∴AC=4$\sqrt{3}$，
∴S_阴影=$\frac{1}{2}$×4×4$\sqrt{3}$-$\frac{60•π•{4}^{2}}{360}$=8$\sqrt{3}$-$\frac{8π}{3}$．

点评 本题考查了平行线的性质，圆周角定理，扇形的面积，三角形的面积，解直角三角形等知识点的综合运用，题目比较好，难度适中．