题目内容
9.m为7+$\sqrt{13}$的小数部分,n为7-$\sqrt{13}$的小数部分,求(m+n)2013的值.分析 首先根据3的平方是9,4的平方是16,估算出$\sqrt{13}$的大小,然后再求得m、n的值,然后再求得m+n的值,最后即可求得答案.
解答 解:∵9<13<16,
∴3<$\sqrt{13}$<4.
∴m=7+$\sqrt{13}$-10=$\sqrt{13}$-3,n=7-$\sqrt{13}$-3=4$-\sqrt{13}$.
∴m+n=$\sqrt{13}$-3+4-$\sqrt{13}$=1.
∴(m+n)2013=12013=1.
点评 本题主要考查的是估算无数的大小,明确一个数的小数部分等于该数减去它的整数部分是解题的关键.

练习册系列答案
相关题目
14. 在直角坐标系中,点B的坐标为(3,1),则点B关于原点成中心对称的点的坐标为( )
在直角坐标系中,点B的坐标为(3,1),则点B关于原点成中心对称的点的坐标为( )
 在直角坐标系中,点B的坐标为(3,1),则点B关于原点成中心对称的点的坐标为( )
在直角坐标系中,点B的坐标为(3,1),则点B关于原点成中心对称的点的坐标为( )| A. | (3,-1) | B. | (-3,1) | C. | (-1,-3) | D. | (-3,-1) |
1.若a满足不等式组$\left\{\begin{array}{l}{2a-1≤1}\\{\frac{1-a}{2}>2}\end{array}\right.$,则关于x的方程(a-2)x2-(2a-1)x+a+$\frac{1}{2}$=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 以上三种情况都有可能 |
18.一组数据:2,3,6,6,7,8,8,8的中位数是( )
| A. | 6 | B. | 6.5 | C. | 7 | D. | 8 |
 如图,x是△ABC一边的长,则x的取值范围是1<x<5.
如图,x是△ABC一边的长,则x的取值范围是1<x<5.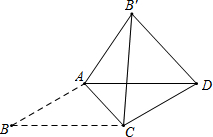 如图,平行四边形ABCD中,∠B=30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D,若AB=2$\sqrt{3}$,∠AB′D=75°,则:①∠CB′D=45°;②BC=3$+\sqrt{3}$.
如图,平行四边形ABCD中,∠B=30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D,若AB=2$\sqrt{3}$,∠AB′D=75°,则:①∠CB′D=45°;②BC=3$+\sqrt{3}$.