Question

11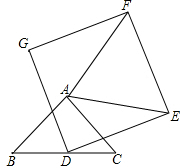．如图，已知△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点，作正方形DEFG，连接AE，若BC=DE=2，将正方形DEFG绕点D逆时针方向旋转，在旋转过程中，当AE为最大值时，求AF的值．

Answer 1

分析 根据旋转可得，当A，D，E三点在一条直线上，且点D在线段AE上时，AE的长有最大值，在Rt△AEF中根据勾股定理求得AF的长．

解答 解：如图，当A，D，E三点在一条直线上，且点D在线段AE上时，AE的长最大，
∵△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点，BC=2，
∴AD=$\frac{1}{2}$BC=1，
此时，AE=AD+DE=1+2=3，
∵正方形DEFG中，∠E=90°，
∴在Rt△AEF中，AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$．

点评 本题以旋转为背景，主要考查了勾股定理以及等腰直角三角形的性质．旋转前、后的图形全等，故对应边相等，对应角相等，这是解决问题的关键．等腰直角三角形具有等腰三角形和直角三角形的所有性质，斜边上中线、角平分线、斜边上的高，三线合一．