题目内容
18. 如图,P是∠AOB内一点,分别在OA、OB边上作点C、D,使得△PCD的周长最小.
如图,P是∠AOB内一点,分别在OA、OB边上作点C、D,使得△PCD的周长最小.
分析 分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于C,交OB于D,△PCD的周长=P1P2.
解答  解:分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于C,交OB于D,;
解:分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于C,交OB于D,;
则OP1=OP=OP2,∠P1OA=∠POA,∠POB=∠P2OB,
CP=P1C,PD=P2D,则△PCD的周长的最小值=P1P2.
点评 本题考查了轴对称最短路线问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合本节所学轴对称变换来解决,多数情况要作点关于某直线的对称点.

练习册系列答案
相关题目
8.沿河两地相距m千米,船在静水中的速度为b千米/时,水流的速度为c千米/时,则船往返一次所需的时间是( )
| A. | $\frac{2m}{b+c}$小时 | B. | ($\frac{m}{b+c}$+$\frac{m}{b-c}$)小时 | C. | $\frac{2m}{b-c}$小时 | D. | ($\frac{m}{b}$+$\frac{m}{c}$)小时 |
3.化简:
| (1)$\sqrt{72}$; | (2)$\sqrt{48}$; | (3)$\sqrt{\frac{2}{3}}$; |
| (4)-2$\sqrt{\frac{9}{2}}$; | (5)$\sqrt{{a}^{3}b}$(a≤0); | (6)$\sqrt{{a}^{4}+2{a}^{2}{b}^{2}+{b}^{4}}$. |
3.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解是( )
| A. | x1=0 x2=4 | B. | x1=1 x2=5 | C. | x1=1 x2=-5 | D. | x1=-1 x2=5 |
4.方程(x-3)(x+4)=0的解是( )
| A. | x=3 | B. | x=-4 | C. | x1=3,x2=-4 | D. | x1=-3,x2=4 |
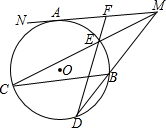 己知:⊙O与直线MN相切于A点,弦BC∥MN,直线MB与⊙O相交于D点,MC与⊙O相交于E,DE的延长线交MN于F点.求证:AF=FM.
己知:⊙O与直线MN相切于A点,弦BC∥MN,直线MB与⊙O相交于D点,MC与⊙O相交于E,DE的延长线交MN于F点.求证:AF=FM.