题目内容
设a,b,c都是正整数,关于x的方程ax2-bx+c=0有两个小于1的不等正数根α,β.
(1)求证:α,β中一个小于 ,另一个大于
,另一个大于 ;
;
(2)求出a的最小值.
(1)证明:由根与系数的关系得:α+β= ,α•β=
,α•β= ,
,
∵(α- )(β-
)(β- )
)
=αβ- (α+β)+
(α+β)+
=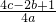 ,
,
∵b2-4ac>0,
∴4a< ,
,
又∵ <1,则4a>ac,
<1,则4a>ac,
∴b>2c,则2(2c-b)<0,
∵b,c都是正整数,
∴2(2c-b)为负偶数,
∴4c-2b+1<0,
∴(α- )(β-
)(β- )=
)=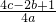 <0,
<0,
∴α,β中一个小于 ,另一个大于
,另一个大于 ;
;
(2)解:∵0<α<1,
∴0<1-α<1,且α≠ ,
,
∴α(1-α)=-α2+α=-(α- )2+
)2+ ,
,
同理β(1-β)< ,
,
∴αβ(1-α)(1-β)< ,
,
∴根据韦达定理得,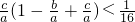 .
.
∵a是正整数,
∴a2>16c(a-b+c),
∵当x=1时,ax2-bx+c=a-b+c>0,a2是正整数的完全平方,
∴a2≥25,猜测a的最小值是5.
事实上,当a=5时,发现方程5x2-5x+1=0的根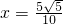 确是小于1的正数,因此可以判断a的最小值等于5.
确是小于1的正数,因此可以判断a的最小值等于5.
分析:(1)根据根与系数的关系得到α+β= ,α•β=
,α•β= ,则(α-
,则(α- )(β-
)(β- )=
)=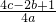 ,根据△的意义得b2-4ac>0,即4a<
,根据△的意义得b2-4ac>0,即4a< ,又
,又 <1,则4a>ac,根据b,c都是正整数,即可得到2(2c-b)为负偶数,可得(α-
<1,则4a>ac,根据b,c都是正整数,即可得到2(2c-b)为负偶数,可得(α- )(β-
)(β- )=
)=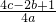 <0,即可得到结论;
<0,即可得到结论;
(2)由0<α<1,得到α(1-α)=-α2+α=-(α- )2+
)2+ ,同理β(1-β)<
,同理β(1-β)< ,则αβ(1-α)(1-β)<
,则αβ(1-α)(1-β)< ,利用根与系数的关系得
,利用根与系数的关系得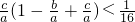 .即a2>16c(a-b+c),当x=1时,ax2-bx+c=a-b+c>0,a2是正整数的完全平方,a2≥25,猜测a的最小值是5.
.即a2>16c(a-b+c),当x=1时,ax2-bx+c=a-b+c>0,a2是正整数的完全平方,a2≥25,猜测a的最小值是5.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=- ,x1•x2=
,x1•x2= .也考查了代数式的变形能力.
.也考查了代数式的变形能力.
 ,α•β=
,α•β= ,
,∵(α-
 )(β-
)(β- )
)=αβ-
 (α+β)+
(α+β)+
=
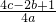 ,
,∵b2-4ac>0,
∴4a<
 ,
,又∵
 <1,则4a>ac,
<1,则4a>ac,∴b>2c,则2(2c-b)<0,
∵b,c都是正整数,
∴2(2c-b)为负偶数,
∴4c-2b+1<0,
∴(α-
 )(β-
)(β- )=
)=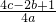 <0,
<0,∴α,β中一个小于
 ,另一个大于
,另一个大于 ;
;(2)解:∵0<α<1,
∴0<1-α<1,且α≠
 ,
,∴α(1-α)=-α2+α=-(α-
 )2+
)2+ ,
,同理β(1-β)<
 ,
,∴αβ(1-α)(1-β)<
 ,
,∴根据韦达定理得,
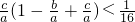 .
.∵a是正整数,
∴a2>16c(a-b+c),
∵当x=1时,ax2-bx+c=a-b+c>0,a2是正整数的完全平方,
∴a2≥25,猜测a的最小值是5.
事实上,当a=5时,发现方程5x2-5x+1=0的根
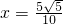 确是小于1的正数,因此可以判断a的最小值等于5.
确是小于1的正数,因此可以判断a的最小值等于5.分析:(1)根据根与系数的关系得到α+β=
 ,α•β=
,α•β= ,则(α-
,则(α- )(β-
)(β- )=
)=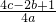 ,根据△的意义得b2-4ac>0,即4a<
,根据△的意义得b2-4ac>0,即4a< ,又
,又 <1,则4a>ac,根据b,c都是正整数,即可得到2(2c-b)为负偶数,可得(α-
<1,则4a>ac,根据b,c都是正整数,即可得到2(2c-b)为负偶数,可得(α- )(β-
)(β- )=
)=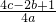 <0,即可得到结论;
<0,即可得到结论;(2)由0<α<1,得到α(1-α)=-α2+α=-(α-
 )2+
)2+ ,同理β(1-β)<
,同理β(1-β)< ,则αβ(1-α)(1-β)<
,则αβ(1-α)(1-β)< ,利用根与系数的关系得
,利用根与系数的关系得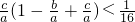 .即a2>16c(a-b+c),当x=1时,ax2-bx+c=a-b+c>0,a2是正整数的完全平方,a2≥25,猜测a的最小值是5.
.即a2>16c(a-b+c),当x=1时,ax2-bx+c=a-b+c>0,a2是正整数的完全平方,a2≥25,猜测a的最小值是5.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .也考查了代数式的变形能力.
.也考查了代数式的变形能力. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目