题目内容
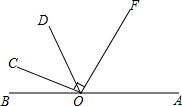如图，已知OF⊥OC，∠BOC：∠COD：∠DOF=1：2：3，求∠AOC的度数．考点：垂线,角的计算
专题：
分析：根据垂线的定义，可得∠COF的度数，根据按比例分配，可得∠COD的度数，根据比例的性质，可得∠BOC的度数，根据邻补角的性质，可得答案．
解答：解：由垂直的定义，得
∠COF=90°，
按比例分配，得
∠COD=90°×
=36°．
∠BOC：∠COD=1：2，
即∠BOC：36°=1：2，由比例的性质，得
∠BOC=18°，
由邻补角的性质，得
∠AOC=180°-∠BOC=180°-18°=162°．
∠COF=90°，
按比例分配，得
∠COD=90°×
| 2 |
| 2+3 |
∠BOC：∠COD=1：2，
即∠BOC：36°=1：2，由比例的性质，得
∠BOC=18°，
由邻补角的性质，得
∠AOC=180°-∠BOC=180°-18°=162°．
点评：本题考查了垂线，利用了垂线的定义，按比例分配，邻补角的性质．
练习册系列答案
相关题目