题目内容
在Rt△ABC中,∠ACB=90°,斜边AB上的中线CD=1,△ABC的周长为2+2
,求△ABC的面积.
| 6 |
考点:二次根式的应用,勾股定理
专题:
分析:首先根据直角三角形斜边上的中线等于斜边的一半求得斜边的长,然后求得两边之和,然后求得两边之积即可求得面积.
解答:解:∵在△ABC中,∠ACB=90°,斜边上的中线CD=1,
∴斜边c的长为:2,
∴两直角边的和为:a+b=2
,
∵a2+b2=c2=4
(a+b)2=a2+b2+2ab
∴2ab=(2
)2-4=20,
∴△ABC面积为:
ab=5.
∴斜边c的长为:2,
∴两直角边的和为:a+b=2
| 6 |
∵a2+b2=c2=4
(a+b)2=a2+b2+2ab
∴2ab=(2
| 6 |
∴△ABC面积为:
| 1 |
| 2 |
点评:本题考查了二次根式的应用、直角三角形斜边上的中线的性质及勾股定理的知识,解题的关键是利用完全平方公式求得两直角边的乘积.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
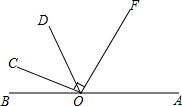 如图,已知OF⊥OC,∠BOC:∠COD:∠DOF=1:2:3,求∠AOC的度数.
如图,已知OF⊥OC,∠BOC:∠COD:∠DOF=1:2:3,求∠AOC的度数. 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.