题目内容
已知?ABCD中,AB=1,E是射线DC上一点,直线AC、BE交于点P,过点P作PQ∥AB,PQ交直线AD于点Q.求:
(1)当点E是DC中点时,求线段PQ的长度;
(2)当点E在线段DC上运动时,设DE=x,PQ=y,求y关于x的解析式;
(3)当DE的长度为多少时,
=
?
(1)当点E是DC中点时,求线段PQ的长度;
(2)当点E在线段DC上运动时,设DE=x,PQ=y,求y关于x的解析式;
(3)当DE的长度为多少时,
| DE |
| PQ |
| 1 |
| 2 |
考点:四边形综合题
专题:
分析:(1)根据平行四边形的性质和平行线分线段成比例定理,得到
=
,求出
=
,再根据DC=1,求出PQ的长;
(2)由DE=x,则EC=1-x,根据PQ∥DC,求出
=
,从而得到关于x、y的等式;
(3)当点E在线段DC的延长线上,且点P在线段AC的反向延长线上时,DE=x,EC=x-1,PQ=2x,根据PQ∥AB∥DE,得到
=
=
,
=
=
,从而有
=
,整理得2x2-4x-1=0,求出x的值.
| PQ |
| DC |
| AP |
| AC |
| AP |
| AC |
| 2 |
| 3 |
(2)由DE=x,则EC=1-x,根据PQ∥DC,求出
| PQ |
| DC |
| AP |
| AC |
(3)当点E在线段DC的延长线上,且点P在线段AC的反向延长线上时,DE=x,EC=x-1,PQ=2x,根据PQ∥AB∥DE,得到
| AC |
| AP |
| DC |
| PQ |
| 1 |
| 2x |
| PA |
| PC |
| AB |
| CE |
| 1 |
| x-1 |
| 2x |
| 2x+1 |
| 1 |
| x-1 |
解答:解:(1)如图1,
∵平行四边形ABCD,AB=1,
∴CD=1,
∵E为CD中点,
∴CE=DE=
,
∵PQ∥DC,
∴
=
,
∵
=2,
∴
=
,
∴
=
,
即PQ=
.
(2)由DE=x,则EC=1-x,
∵PQ∥DC,
∴
=
,
∵
=
,
∴
=
,
∴y=
(0≤x≤1).
(3)Ⅰ)点E在线段DC上时,根据y=
,又
=
,
∴2x=
,
即2x2-4x+1=0,解得x=
,
又0≤x≤1,
∴x=
.
Ⅱ)如图2,点E在线段DC的延长线上,且点P在线段AC的延长线上时,
DE=x,EC=x-1,PQ=2x,
∵PQ∥AB∥DE,
∴
=
=
,
=
=
,
又
+
=1,即
+x-1=1,
解得x=
,又x>1,
∴x=
.
Ⅲ)如图3,当点E在线段DC的延长线上,且点P在线段AC的反向延长线上时,DE=x,EC=x-1,PQ=2x,
∵PQ∥AB∥DE,
∴
=
=
,
=
=
,
∴
=
,
∴2x2-4x-1=0,
解得x=
,
又x>1,
∴x=
,
综上,符合条件的DE长度
可以为
,
.

∵平行四边形ABCD,AB=1,
∴CD=1,
∵E为CD中点,
∴CE=DE=
| 1 |
| 2 |
∵PQ∥DC,
∴
| PQ |
| DC |
| AP |
| AC |
∵
| AP |
| PC |
∴
| AP |
| AC |
| 2 |
| 3 |
∴
| PQ |
| 1 |
| 2 |
| 3 |
即PQ=
| 2 |
| 3 |
(2)由DE=x,则EC=1-x,
∵PQ∥DC,
∴
| PQ |
| DC |
| AP |
| AC |
∵
| AP |
| CP |
| 1 |
| 1-x |
∴
| AP |
| AC |
| 1 |
| 2-x |
∴y=
| 1 |
| 2-x |
(3)Ⅰ)点E在线段DC上时,根据y=
| 1 |
| 2-x |
| DE |
| PQ |
| 1 |
| 2 |
∴2x=
| 1 |
| 2-x |
即2x2-4x+1=0,解得x=
2±
| ||
| 2 |

又0≤x≤1,
∴x=
2-
| ||
| 2 |
Ⅱ)如图2,点E在线段DC的延长线上,且点P在线段AC的延长线上时,
DE=x,EC=x-1,PQ=2x,
∵PQ∥AB∥DE,
∴
| AC |
| AP |
| DC |
| PQ |
| 1 |
| 2x |
| PC |
| PA |
| CE |
| AB |
| x-1 |
| 1 |
又
| AC |
| AP |
| PC |
| PA |
| 1 |
| 2x |

解得x=
2±
| ||
| 2 |
∴x=
2+
| ||
| 2 |
Ⅲ)如图3,当点E在线段DC的延长线上,且点P在线段AC的反向延长线上时,DE=x,EC=x-1,PQ=2x,
∵PQ∥AB∥DE,
∴
| AC |
| AP |
| DC |
| PQ |
| 1 |
| 2x |
| PA |
| PC |
| AB |
| CE |
| 1 |
| x-1 |
∴
| 2x |
| 2x+1 |
| 1 |
| x-1 |
∴2x2-4x-1=0,
解得x=
2±
| ||
| 2 |
又x>1,
∴x=
2+
| ||
| 2 |
综上,符合条件的DE长度
可以为
2±
| ||
| 2 |
2+
| ||
| 2 |
点评:本题主要考查了四边形的性质,同时涉及平行线分线段成比例定理、动点问题、函数、分类讨论等考点,内容复杂,是经典题目.

练习册系列答案
相关题目
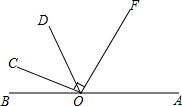 如图,已知OF⊥OC,∠BOC:∠COD:∠DOF=1:2:3,求∠AOC的度数.
如图,已知OF⊥OC,∠BOC:∠COD:∠DOF=1:2:3,求∠AOC的度数.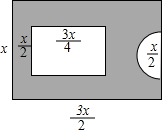 某中学一寝室前有一块长为
某中学一寝室前有一块长为