题目内容
在四边形ABCD中,∠ADC=120°,AB⊥AD,BC⊥CD,AB=5
,CD=3
,求四边形ABCD的面积.
| 3 |
| 3 |
考点:解直角三角形
专题:
分析:过A作AE⊥BC于E,过D作DF⊥AE于F,求得四边形DCEF为矩形,根据直角三角函数求得AE、BE,根据△ADF∽△BAE,求得DF,进而求得三角形ABE和梯形ADCE的面积,这两个面积的和就是四边形ABCD的面积.
解答: 解:过A作AE⊥BC于E,过D作DF⊥AE于F,
解:过A作AE⊥BC于E,过D作DF⊥AE于F,
∵∠ADC=120°,AB⊥AD,BC⊥CD,
∴∠B=60°
∵AB=5
,
∴AE=AB×sinB=AB×sin60°=7.5,BE=AB×cosB=AB×cos60°=
,
∴S△ABE=
×AE×BE=
,
∵AE⊥BC,DF⊥AE,BC⊥CD,
∴四边形DCEF为矩形,
∴EF=CD=3
,
∴AF=AE-EF=7.5-3
=
,
∵∠BAE+∠DAF=90°,∠B+∠BAE=90°,
∴∠B=∠DAF,
∵∠AFD=∠AEB=90°,
∴△ADF∽△BAE,
∴
=
,
即
=
,
解得:DF=
∴S梯形ADCE=
(DC+AE)×DF=
(3
+
)×
=
,
∴S=S△ABE+S梯形ADCE=
+
=
;
∴四边形ABCD的面积为
.
 解:过A作AE⊥BC于E,过D作DF⊥AE于F,
解:过A作AE⊥BC于E,过D作DF⊥AE于F,∵∠ADC=120°,AB⊥AD,BC⊥CD,
∴∠B=60°
∵AB=5
| 3 |
∴AE=AB×sinB=AB×sin60°=7.5,BE=AB×cosB=AB×cos60°=
5
| ||
| 2 |
∴S△ABE=
| 1 |
| 2 |
75
| ||
| 8 |
∵AE⊥BC,DF⊥AE,BC⊥CD,
∴四边形DCEF为矩形,
∴EF=CD=3
| 3 |
∴AF=AE-EF=7.5-3
| 3 |
15-6
| ||
| 2 |
∵∠BAE+∠DAF=90°,∠B+∠BAE=90°,
∴∠B=∠DAF,
∵∠AFD=∠AEB=90°,
∴△ADF∽△BAE,
∴
| DF |
| AE |
| AF |
| BE |
即
| DF | ||
|
| ||||
|
解得:DF=
15
| ||
| 2 |
∴S梯形ADCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 15 |
| 2 |
15
| ||
| 2 |
30+129
| ||
| 8 |
∴S=S△ABE+S梯形ADCE=
75
| ||
| 8 |
30+129
| ||
| 8 |
30+204
| ||
| 8 |
∴四边形ABCD的面积为
30+204
| ||
| 8 |
点评:本题考查了解直角三角形,矩形的判定和性质,三角形相似的判定和性质以及三角形的面积、梯形的面积等,过A作AE⊥BC于E,过D作DF⊥AE于F,构建直角三角形和梯形时本题的关键;

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 用平面截下列几何体,相应的截面形状是( )
用平面截下列几何体,相应的截面形状是( )A、 |
B、 |
C、 |
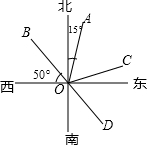 如图,OA的方向是北偏东15°,OB的方向是西偏北50°.
如图,OA的方向是北偏东15°,OB的方向是西偏北50°. 如图,x轴、y轴分别平分∠DBC、∠EAD,求∠AED+∠BCD的值.
如图,x轴、y轴分别平分∠DBC、∠EAD,求∠AED+∠BCD的值.