题目内容
 如图,在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则不能添加的条件是( )
如图,在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则不能添加的条件是( )| A、AD∥BC |
| B、AB=DC |
| C、∠A=∠C |
| D、AD=BC |
考点:平行四边形的判定
专题:
分析:根据平行四边形的判定方法,逐项判断即可.
解答:解:A、AB∥CD,AD∥BC,两组对边分别平行,可证明四边形ABCD为平行四边形;
B、AB∥CD,AB=DC,一组对边分别平行且相等,可证明四边形ABCD为平行四边形;
C、由AB∥CD可得∠A+∠D=180°,又∠A=∠C,所以可得∠C+∠D=180°,所以AD∥BC,所以四边形ABCD为平行四边形;
D、当AB∥CD,AD=BC时,四边形ABCD可能为等腰梯形,所以不能证明四边形ABCD为平行四边形;
故选D.
B、AB∥CD,AB=DC,一组对边分别平行且相等,可证明四边形ABCD为平行四边形;
C、由AB∥CD可得∠A+∠D=180°,又∠A=∠C,所以可得∠C+∠D=180°,所以AD∥BC,所以四边形ABCD为平行四边形;
D、当AB∥CD,AD=BC时,四边形ABCD可能为等腰梯形,所以不能证明四边形ABCD为平行四边形;
故选D.
点评:本题主要考查平行四边形的判定方法,掌握平行四边形的判定方法是解题的关键.平行四边形的判定方法有:①两组对边分别平行,②两组对边分别相等,③一组对边平行且相等,④两组对角分别相等,⑤对角线互相平分.

练习册系列答案
相关题目
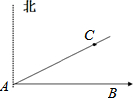 如图,测得A点到灯塔C点的距离为10海里,灯塔C点在A点东偏北30°方向上,一轮船由A点出发向正东方向航行,当此轮船行至距A点
如图,测得A点到灯塔C点的距离为10海里,灯塔C点在A点东偏北30°方向上,一轮船由A点出发向正东方向航行,当此轮船行至距A点