题目内容
已知Rt△ABC中,∠A=30°,∠C=90°,AB=12,D为射线AB上一动点,经过点C的⊙O与直线AB相切于点D,交射线AC于点E.
(1)如图1,当点O在边AC上时,求⊙O的半径;
(2)如图2,当CD平分∠ACB,求⊙O的半径;
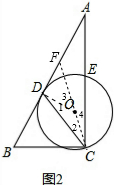
(3)如图3,当D为线段AB延长线上一点,且CD=
BC时,则DE的值为 (直接写出结果).
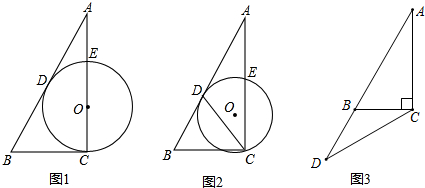
(1)如图1,当点O在边AC上时,求⊙O的半径;
(2)如图2,当CD平分∠ACB,求⊙O的半径;
(3)如图3,当D为线段AB延长线上一点,且CD=
| 3 |

考点:圆的综合题
专题:综合题
分析:(1)连结OD,如图1,设⊙O的半径为r,利用含30度的直角三角形三边的关系得到BC=
AB=6,AC=
BC=6
,再根据切线的性质得∠ADO=90°,在Rt△ADO中由于OD=
AO,则r=
(6
-r),即可解得r=2
;
(2)延长CO交AB于F,连结OD,如图2,设⊙O的半径为r,根据切线的性质得∠FDO=90°,再利用角平分线定义得到∠ACD=45°,由三角形外角性质有∠BDC=∠A+∠ACD=75°,则∠1=15°,所以∠1=∠2=15°,
可计算出∠3=30°,∠4=30°,于是有FA=FC,接着证明∠FCB=∠B得到FC=FB,所以FC=
AB=6;在Rt△ODE中,利用含30度的直角三角形三边的关系得到DF=
r,OF=2DF=
r,然后根据CF=OC+OF得到
r+r=6,再解方程求出r即可;
(3)连结OD、OC,作DH⊥AE于H,如图3,根据切线的性质得∠ADO=90°,再由CD=
BC=6
得到CA=CD,
则∠ADC=∠A=30°,于是可计算出∠ODC=90°-∠ADC=60°,从而判断△ODC为等边三角形,得到∠COD=60°,根据圆周角定理得∠E=
∠COD=30°,接着证明BD=BC=6,然后证明△ABC∽△ADH,利用相似比计算出DH=9,最后在Rt△EDH中利用含30度的直角三角形三边的关系求DE.
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)延长CO交AB于F,连结OD,如图2,设⊙O的半径为r,根据切线的性质得∠FDO=90°,再利用角平分线定义得到∠ACD=45°,由三角形外角性质有∠BDC=∠A+∠ACD=75°,则∠1=15°,所以∠1=∠2=15°,
可计算出∠3=30°,∠4=30°,于是有FA=FC,接着证明∠FCB=∠B得到FC=FB,所以FC=
| 1 |
| 2 |
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
(3)连结OD、OC,作DH⊥AE于H,如图3,根据切线的性质得∠ADO=90°,再由CD=
| 3 |
| 3 |
则∠ADC=∠A=30°,于是可计算出∠ODC=90°-∠ADC=60°,从而判断△ODC为等边三角形,得到∠COD=60°,根据圆周角定理得∠E=
| 1 |
| 2 |
解答:解:(1)连结OD,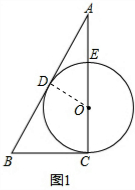 如图1,设⊙O的半径为r,
如图1,设⊙O的半径为r,
∵∠A=30°,∠C=90°,AB=12,
∴BC=
AB=6,AC=
BC=6
,
∵经过点C的⊙O与直线AB相切于点D,
∴OD⊥AD,
∴∠ADO=90°,
在Rt△ADO中,∵∠A=30°,
∴OD=
AO,即r=
(6
-r),解得r=2
,
即⊙O的半径为2
;
(2) 延长CO交AB于F,连结OD,如图2,设⊙O的半径为r,
延长CO交AB于F,连结OD,如图2,设⊙O的半径为r,
∵经过点C的⊙O与直线AB相切于点D,
∴OD⊥AD,
∴∠FDO=90°,
∵CD平分∠ACB,
∴∠ACD=45°,
∴∠BDC=∠A+∠ACD=75°,
∴∠1=90°-∠BDC=15°,
而OD=OC,
∴∠1=∠2=15°,
∴∠3=30°,∠4=∠ACD-∠2=30°,
∴FA=FC,
∵∠FCB=90°-∠4=60°=∠B,
∴FC=FB,
∴FC=
AB=6,
在Rt△ODE中,∵∠3=30°,OD=r,
∴DF=
r,
∴OF=2DF=
r,
∴CF=OC+OF,
即
r+r=6,解得r=12
-18,
即⊙O的半径为12
-18;
(3)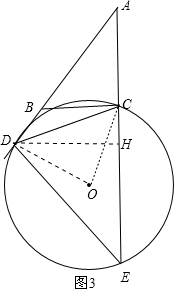 连结OD、OC,作DH⊥AE于H,如图3,
连结OD、OC,作DH⊥AE于H,如图3,
∵经过点C的⊙O与直线AB相切于点D,
∴OD⊥AD,
∴∠ADO=90°,
∵CD=
BC=6
,
∴CA=CD,
∴∠ADC=∠A=30°,
∴∠ODC=90°-∠ADC=60°,
而OD=OC,
∴△ODC为等边三角形,
∴∠COD=60°,
∴∠E=
∠COD=30°,
∵∠ABC=∠BDC+∠BCD=60°,
而∠BDC=30°,
∴∠BCD=30°,
∴BD=BC=6,
∵DH∥BC,
∴△ABC∽△ADH,
∴
=
,即
=
,解得DH=9,
在Rt△EDH中,∵∠E=30°,
∴DE=2DH=18.
故答案为18.
 如图1,设⊙O的半径为r,
如图1,设⊙O的半径为r,∵∠A=30°,∠C=90°,AB=12,
∴BC=
| 1 |
| 2 |
| 3 |
| 3 |
∵经过点C的⊙O与直线AB相切于点D,
∴OD⊥AD,
∴∠ADO=90°,
在Rt△ADO中,∵∠A=30°,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
即⊙O的半径为2
| 3 |
(2)
 延长CO交AB于F,连结OD,如图2,设⊙O的半径为r,
延长CO交AB于F,连结OD,如图2,设⊙O的半径为r,∵经过点C的⊙O与直线AB相切于点D,
∴OD⊥AD,
∴∠FDO=90°,
∵CD平分∠ACB,
∴∠ACD=45°,
∴∠BDC=∠A+∠ACD=75°,
∴∠1=90°-∠BDC=15°,
而OD=OC,
∴∠1=∠2=15°,
∴∠3=30°,∠4=∠ACD-∠2=30°,
∴FA=FC,
∵∠FCB=90°-∠4=60°=∠B,
∴FC=FB,
∴FC=
| 1 |
| 2 |
在Rt△ODE中,∵∠3=30°,OD=r,
∴DF=
| ||
| 3 |
∴OF=2DF=
2
| ||
| 3 |
∴CF=OC+OF,
即
2
| ||
| 3 |
| 3 |
即⊙O的半径为12
| 3 |
(3)
 连结OD、OC,作DH⊥AE于H,如图3,
连结OD、OC,作DH⊥AE于H,如图3,∵经过点C的⊙O与直线AB相切于点D,
∴OD⊥AD,
∴∠ADO=90°,
∵CD=
| 3 |
| 3 |
∴CA=CD,
∴∠ADC=∠A=30°,
∴∠ODC=90°-∠ADC=60°,
而OD=OC,
∴△ODC为等边三角形,
∴∠COD=60°,
∴∠E=
| 1 |
| 2 |
∵∠ABC=∠BDC+∠BCD=60°,
而∠BDC=30°,
∴∠BCD=30°,
∴BD=BC=6,
∵DH∥BC,
∴△ABC∽△ADH,
∴
| BC |
| DH |
| AB |
| AD |
| 6 |
| DH |
| 12 |
| 12+6 |
在Rt△EDH中,∵∠E=30°,
∴DE=2DH=18.
故答案为18.
点评:本题考查了圆的综合题:熟练掌握圆周角定理、切线性质和等腰三角形的性质;会利用含30度的直角三角形三边的关系和相似比进行几何计算.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
以下四家银行的行标图中,是轴对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
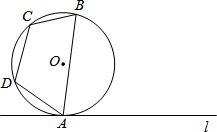 如图,⊙O的半径为3,四边形ABCD是⊙O的内接四边形,直线l与⊙O相切于点A,若∠A=60°,∠D=110°,
如图,⊙O的半径为3,四边形ABCD是⊙O的内接四边形,直线l与⊙O相切于点A,若∠A=60°,∠D=110°, |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
若
=
,则下列各式不成立的是( )
| x |
| y |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知△ABC的三边长分别为1、5、x,周长为整数,则△ABC的形状是( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
下列长度的各组线段中,能组成三角形的是( )
| A、5cm,9cm,3cm |
| B、3cm,11cm,8cm |
| C、6.3cm,6.3cm,4.4cm |
| D、15cm,8cm,6cm |
 如图,⊙O的内接四边形ABCD中,∠BCD=138°,则∠BOD的度数是
如图,⊙O的内接四边形ABCD中,∠BCD=138°,则∠BOD的度数是