题目内容
如图，∠BAD=∠C，DE⊥AB于E，AF⊥BC于F，若BD=6，AB=8，则DE：AF=________．
3：4
分析：要求DE：AF的值，又已知BD=6，AB=8且DE、AF、BD、AB分别是两个直角三角形△BED和△BFA中的边，所以只要证明△BED∽△BFA即可，根据相似三角形的性质；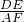
=
=
=
．
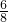解答：∵DE⊥AB，AF⊥BC
∴∠BED=∠BFA
又∵∠B=∠B
∴△BED∽△BFA
∴==．
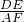即：DE：AF=3：4．
点评：本题主要考查利用相似三角形的性质求边之比，关键在于找出可以判定两个三角形相似的条件．
分析：要求DE：AF的值，又已知BD=6，AB=8且DE、AF、BD、AB分别是两个直角三角形△BED和△BFA中的边，所以只要证明△BED∽△BFA即可，根据相似三角形的性质；
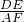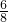===．解答：∵DE⊥AB，AF⊥BC
∴∠BED=∠BFA
又∵∠B=∠B
∴△BED∽△BFA
∴
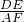==．即：DE：AF=3：4．
点评：本题主要考查利用相似三角形的性质求边之比，关键在于找出可以判定两个三角形相似的条件．
练习册系列答案
相关题目
3、如图，∠BAD=∠CAE，∠B=∠D，AB=2AD，若BC=3cm，则DE=
如图，∠BAD=90°，∠DBC=90°，AD=3，AB=4，CD=13，求四边形ABCD的面积．
如图，∠BAD与∠BCD的一边相交于点O，AM、CM分别平分∠BAD和∠BCD，并相交于点M，AM交BC于点E，CM交AD于点F．
如图，∠BAD=∠CAE，AB=AD，AC=AE．
如图，∠BAD=∠CAE，∠B=∠D，且AB=AD，求证：AC=AE．